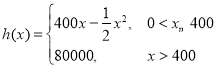题目内容
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)讨论函数![]() 的单调性.
的单调性.
【答案】(Ⅰ)![]() ;(Ⅱ)分类讨论,详见解析.
;(Ⅱ)分类讨论,详见解析.
【解析】
(Ⅰ)先由题设条件求得![]() ,再由导数的几何意义求得
,再由导数的几何意义求得![]() 在
在![]() 处的切线的斜率
处的切线的斜率![]() (1),进而求得切线方程;
(1),进而求得切线方程;
(Ⅱ)先求导,再对![]() 分成:①
分成:①![]() 当
当![]() 时;②
时;②![]() 当
当![]() 时;③
时;③![]() 当
当![]() 时;④
时;④![]() 当
当![]() 时;进行讨论,得出结果.
时;进行讨论,得出结果.
(Ⅰ)![]() 已知函数
已知函数![]() ,
,
则![]() 的定义域为:
的定义域为:![]() ,
,
![]() ,
,
则![]() (1)
(1)![]() ,又
,又![]() (1)
(1)![]() ,
,
![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
(Ⅱ)由(Ⅰ)知:![]() ,
,
![]() ①当
①当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 时单调递增,在
时单调递增,在![]() ,
,![]() 时单调递减;
时单调递减;
②当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 时单调递增;
时单调递增;
③当![]() 时,令
时,令![]() ,有
,有![]() ,或
,或![]() ,
,
此时![]() 在
在![]() 与
与![]() 时单调递增,在
时单调递增,在![]() 单调递减;
单调递减;
④当![]() 时,
时,![]() 在
在![]() 与
与![]() ,
,![]() 时单调递增,在
时单调递增,在![]() ,
,![]() 时单调递减;
时单调递减;
⑤当![]() 时,
时,![]() 在
在![]() 时单调递增,在
时单调递增,在![]() ,
,![]() 时单调递减;
时单调递减;
综上可知:
当![]() 时,
时,![]() 在
在![]() 时单调递增,在
时单调递增,在![]() ,
,![]() 时单调递减;
时单调递减;
当![]() 时,
时,![]() 在
在![]() 与
与![]() ,
,![]() 时单调递增,在
时单调递增,在![]() ,
,![]() 时单调递减;
时单调递减;
当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 时单调递增;
时单调递增;
当![]() 时,
时,![]() 在
在![]() 与
与![]() 时单调递增,在
时单调递增,在![]() 单调递减.
单调递减.

练习册系列答案
相关题目
【题目】某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分为5组:![]()
![]()
![]() 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.
(I)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的概率;
(II)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
![]()
![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
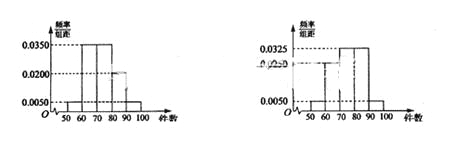
25周岁以上组 25周岁以下组