题目内容
已知函数f(x)=loga[(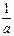 -2)x+1]在区间[1,2]上恒为正,求实数a的取值范围.
-2)x+1]在区间[1,2]上恒为正,求实数a的取值范围.
解:∵f(x)=loga[( ①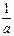 -2)x+1]在[1,2]上恒正,……………………2分
-2)x+1]在[1,2]上恒正,……………………2分
(1)当 a>1
a>1 时,真数μ=(
时,真数μ=(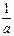 -2)x+1>1,
-2)x+1>1,
∴(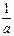 -2)x>0,∴
-2)x>0,∴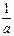 -2>0即a<
-2>0即a<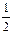 (舍) .………………………………6分
(舍) .………………………………6分
(2)当0<a<1时,0<μ<1
∴
②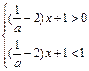
要使①式当x∈[1,2]恒成立,则
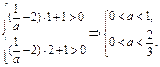 ∴0<a<
∴0<a<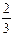 .
.要使②式成立,则(
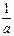 -2)x<0,只要
-2)x<0,只要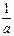 -2<0,∴
-2<0,∴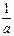 <2 ,∴a>
<2 ,∴a>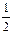 .
.综上
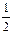 <a<
<a<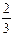 .………………………………12分
.………………………………12分
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数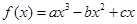 的图象如图所示,且
的图象如图所示,且 在
在 与
与 处取得极值,给出下列判断:
处取得极值,给出下列判断: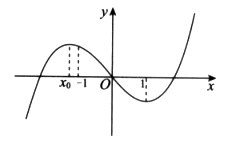
①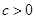 ;
;
②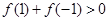 ;
;
③函数 在区间
在区间 上是增函数。
上是增函数。
其中正确的判断是( )
| A.①③ | B.② | C.②③ | D.①② |
抛物线 在点
在点 处的切线的倾斜角是( )
处的切线的倾斜角是( )
A.30 | B.45 | C.60 | D.90 |

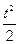 (0≤t≤5),其中t为产品售出的数量(单位:百件).
(0≤t≤5),其中t为产品售出的数量(单位:百件).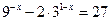 (2)
(2)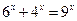
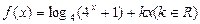 为偶函数.
为偶函数. 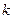 的值;
的值;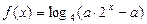 有且只有一个根, 求实数
有且只有一个根, 求实数 的取值范围.
的取值范围.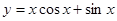 的部分图象大致为( ).
的部分图象大致为( ).