题目内容
变量x、y满足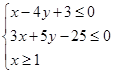
(1)假设z =4x-3y,求z的最大值.
(2)设z =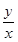 ,求z的最小值.
,求z的最小值.
(3)设z =x2+y2,求z的取值范围.
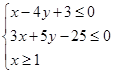
(1)假设z =4x-3y,求z的最大值.
(2)设z =
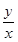 ,求z的最小值.
,求z的最小值.(3)设z =x2+y2,求z的取值范围.
(1)zmax=14;(2)zmax=koB=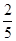 ;(3)z
;(3)z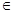
 .
.
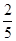 ;(3)z
;(3)z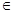
 .
.(1)作出不等式表示的可行域,然后根据直线z=4x-3y与在y轴的截距是正相关,还是负相关来确定最优解,从而求得最大值.
(2)注意利用其几何意义 z =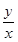 ,它表示可行域内的点与原点连线的斜率的大小.注意数形结合即可求解.
,它表示可行域内的点与原点连线的斜率的大小.注意数形结合即可求解.
(3) z =x2+y2它的几何意义是可行域内的点到原点距离的平方,利用它然后数形结合即可.
解:联立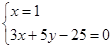
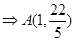
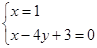
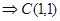

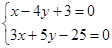
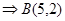 4’
4’
(1)zmax=14 6’
(2)zmax=koB=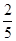 9’
9’
(3)z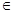
 13’
13’
(2)注意利用其几何意义 z =
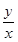 ,它表示可行域内的点与原点连线的斜率的大小.注意数形结合即可求解.
,它表示可行域内的点与原点连线的斜率的大小.注意数形结合即可求解.(3) z =x2+y2它的几何意义是可行域内的点到原点距离的平方,利用它然后数形结合即可.
解:联立
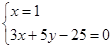
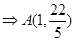
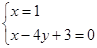
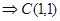

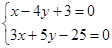
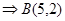 4’
4’(1)zmax=14 6’
(2)zmax=koB=
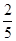 9’
9’ (3)z
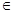
 13’
13’
练习册系列答案
相关题目
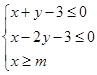 ,则实数m的最大值为
,则实数m的最大值为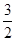
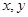 满足
满足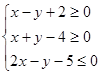 ,则
,则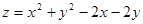 的最大值和最小值分别是()
的最大值和最小值分别是()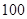 和
和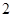
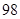 和
和
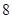 和
和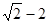
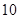 和
和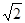
 的取值范围为
的取值范围为 

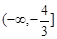
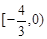
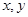 满足约束条件:
满足约束条件: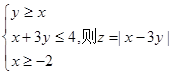 的最大值为( )
的最大值为( ) 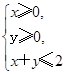 确定的平面区域内,则点N(a+b,a-b)所在平面区域的面积是
确定的平面区域内,则点N(a+b,a-b)所在平面区域的面积是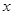 和
和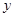 满足约束条件
满足约束条件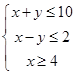 ,则
,则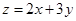 的最小值为( )
的最小值为( )

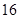
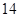
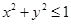 ,则点
,则点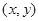 不在区域
不在区域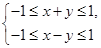 内的概率是( )
内的概率是( )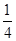
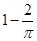
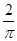
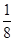
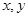 满足约束条件:
满足约束条件: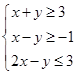 ,则目标函数
,则目标函数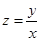 的最小值为 .
的最小值为 .