题目内容
已知函数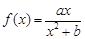 在
在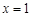 处取得极值2.
处取得极值2.
⑴ 求函数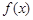 的解析式;
的解析式;
⑵ 若函数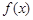 在区间
在区间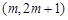 上是单调函数,求实数m的取值范围;
上是单调函数,求实数m的取值范围;
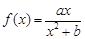 在
在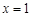 处取得极值2.
处取得极值2.⑴ 求函数
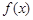 的解析式;
的解析式;⑵ 若函数
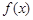 在区间
在区间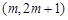 上是单调函数,求实数m的取值范围;
上是单调函数,求实数m的取值范围;⑴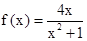 ⑵
⑵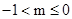 或
或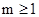
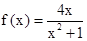 ⑵
⑵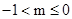 或
或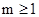
第一问中利用导数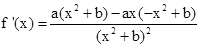
又f(x)在x=1处取得极值2,所以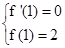 ,
,
所以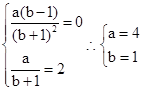
第二问中,
因为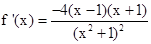 ,又f(x)的定义域是R,所以由
,又f(x)的定义域是R,所以由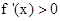 ,得-1<x<1,所以f(x)在[-1,1]上单调递增,在
,得-1<x<1,所以f(x)在[-1,1]上单调递增,在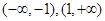 上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有
上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有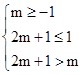 ,得
,得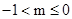
解:⑴ 求导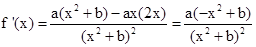 ,又f(x)在x=1处取得极值2,所以
,又f(x)在x=1处取得极值2,所以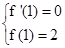 ,即
,即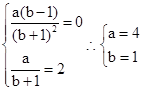 ,所以
,所以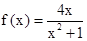 …………6分
…………6分
⑵ 因为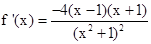 ,又f(x)的定义域是R,所以由
,又f(x)的定义域是R,所以由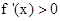 ,得-1<x<1,所以f(x)在[-1,1]上单调递增,在
,得-1<x<1,所以f(x)在[-1,1]上单调递增,在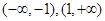 上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有
上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有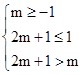 ,得
,得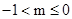 , …………9分
, …………9分
当f(x)在区间(m,2m+1)上单调递减,则有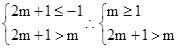
得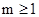 …………12分
…………12分
.综上所述,当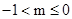 时,f(x)在(m,2m+1)上单调递增,当
时,f(x)在(m,2m+1)上单调递增,当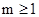 时,f(x)在(m,2m+1)上单调递减;则实数m的取值范围是
时,f(x)在(m,2m+1)上单调递减;则实数m的取值范围是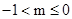 或
或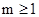
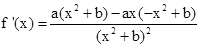
又f(x)在x=1处取得极值2,所以
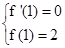 ,
,所以
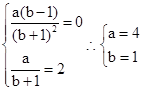
第二问中,
因为
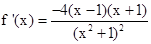 ,又f(x)的定义域是R,所以由
,又f(x)的定义域是R,所以由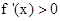 ,得-1<x<1,所以f(x)在[-1,1]上单调递增,在
,得-1<x<1,所以f(x)在[-1,1]上单调递增,在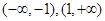 上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有
上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有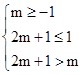 ,得
,得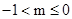
解:⑴ 求导
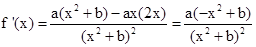 ,又f(x)在x=1处取得极值2,所以
,又f(x)在x=1处取得极值2,所以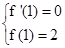 ,即
,即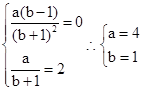 ,所以
,所以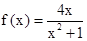 …………6分
…………6分⑵ 因为
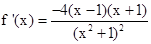 ,又f(x)的定义域是R,所以由
,又f(x)的定义域是R,所以由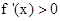 ,得-1<x<1,所以f(x)在[-1,1]上单调递增,在
,得-1<x<1,所以f(x)在[-1,1]上单调递增,在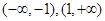 上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有
上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有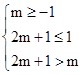 ,得
,得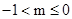 , …………9分
, …………9分当f(x)在区间(m,2m+1)上单调递减,则有
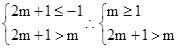
得
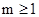 …………12分
…………12分.综上所述,当
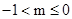 时,f(x)在(m,2m+1)上单调递增,当
时,f(x)在(m,2m+1)上单调递增,当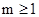 时,f(x)在(m,2m+1)上单调递减;则实数m的取值范围是
时,f(x)在(m,2m+1)上单调递减;则实数m的取值范围是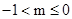 或
或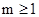

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
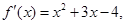 则
则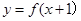 的单调减区间
的单调减区间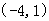
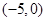
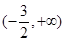
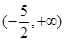
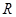 上的可导函数
上的可导函数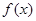 ,当
,当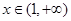 时,
时,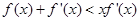 恒成立,
恒成立,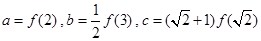 ,则
,则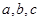 的大小关系为 ( )
的大小关系为 ( )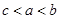

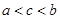
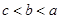
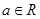 ,函数
,函数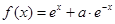 的导函数是
的导函数是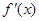 ,且
,且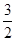 ,则切点的横坐标是( )
,则切点的横坐标是( ) 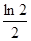
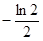
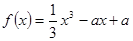
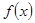 恰好有两个不同的零点,求
恰好有两个不同的零点,求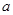 的值。
的值。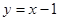 相切,求
相切,求
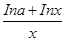 在[1,+∞)上为减函数,求实数a的取值范围.
在[1,+∞)上为减函数,求实数a的取值范围.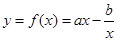 在点
在点 处的切线方程为
处的切线方程为 ,则
,则 的值为 ( )
的值为 ( ) 



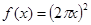 的导数
的导数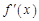 =__________
=__________