题目内容
15.已知双曲线x2-$\frac{{y}^{2}}{3}$=1的一条渐近线与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{a}^{2}-4}$=1相交与点P,若|OP|=2,则椭圆离心率为( )| A. | $\sqrt{3}$-1 | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
分析 先根据双曲线x2-$\frac{{y}^{2}}{3}$=1得出它的一条渐近线方程为:y=$\sqrt{3}$x,其倾斜角为60°,从而得到∠POx=60°又|OP|=2,故可得P点的坐标,将P的坐标代入椭圆方程得a从而求出椭圆的离心率.
解答 解:根据双曲线x2-$\frac{{y}^{2}}{3}$=1得出它的一条渐近线方程为:y=$\sqrt{3}$x,其倾斜角为60°,
设这条渐近线与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{a}^{2}-4}$=1相交于点P,
则∠POx=60°且|OP|=2,故可得P点的坐标为(1,$\sqrt{3}$).
代入椭圆方程得:$\frac{1}{{a}^{2}}+\frac{3}{{a}^{2}-4}$=1,⇒a=$\sqrt{3}$+1或a=$\sqrt{3}$-1<2(不合,舍去)
∴椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{a}^{2}-4}$=1的a=$\sqrt{3}$+1,b2=2$\sqrt{3}$,
∴c=2,
则椭圆的离心率为e=$\frac{c}{a}$=$\sqrt{3}$-1.
故选:A.
点评 本小题主要考查椭圆的简单性质、双曲线的简单性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,属于基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
7.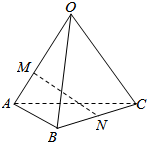 如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}$=$\frac{2}{3}$$\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于( )
如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}$=$\frac{2}{3}$$\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于( )
 如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}$=$\frac{2}{3}$$\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于( )
如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}$=$\frac{2}{3}$$\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于( )| A. | $\frac{1}{2}\vec a-\frac{2}{3}\vec b+\frac{1}{2}\vec c$ | B. | $-\frac{2}{3}\vec a+\frac{1}{2}\vec b+\frac{1}{2}\vec c$ | C. | $\frac{1}{2}\vec a+\frac{1}{2}\vec b-\frac{1}{2}\vec c$ | D. | $\frac{2}{3}\vec a+\frac{2}{3}\vec b-\frac{1}{2}\vec c$ |