题目内容
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
从数列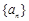 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列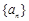 的一个子数列.
的一个子数列.
设数列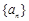 是一个首项为
是一个首项为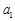 、公差为
、公差为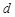
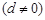 的无穷等差数列.
的无穷等差数列.
(1)若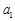 ,
,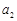 ,
,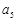 成等比数列,求其公比
成等比数列,求其公比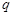 .
.
(2)若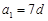 ,从数列
,从数列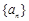 中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为
中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为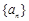 的无穷等比子数列,请说明理由.
的无穷等比子数列,请说明理由.
(3)若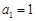 ,从数列
,从数列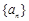 中取出第1项、第
中取出第1项、第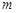
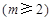 项(设
项(设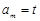 )作为一个等比数列的第1项、第2项.求证:当
)作为一个等比数列的第1项、第2项.求证:当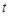 为大于1的正整数时,该数列为
为大于1的正整数时,该数列为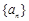 的无穷等比子数列.
的无穷等比子数列.
【答案】
略
【解析】(1)解:由题设,得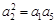 ,即
,即 ,得
,得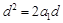 ,又
,又 ,于是
,于是 ,故其公比
,故其公比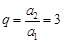 .(4分)
.(4分)
(2)解:设等比数列为 ,其公比
,其公比 ,
, ,(6分)
,(6分)
由题设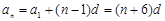 .
.
假设数列 为
为 的无穷等比子数列,则对任意自然数
的无穷等比子数列,则对任意自然数
 ,都存在
,都存在 ,使
,使 ,
,
即 ,得
,得 ,(8分)
,(8分)
当 时,
时,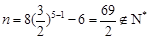 ,与假设矛盾,
,与假设矛盾,
故该数列不为 的无穷等比子数列.(10分)
的无穷等比子数列.(10分)
(3)即证明无穷等比数列 中的每一项均为数列
中的每一项均为数列 中的项.
中的项.
在等比数列 中,
中, ,(12分)[来源:]
,(12分)[来源:]
在等差数列 中,
中,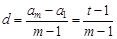 ,
, ,(14分)
,(14分)
若 为数列
为数列 中的第
中的第 项,则由
项,则由 ,得
,得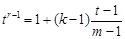 ,
,
整理得 ,(16分)[来源:]
,(16分)[来源:]
由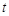 ,
,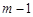 均为正整数,得
均为正整数,得 也为正整数,
也为正整数,
故无穷等比数列 中的每一项均为数列
中的每一项均为数列 中的项,得证.(18分)
中的项,得证.(18分)

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为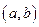 ,点
,点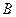 的坐标为
的坐标为 ,其中
,其中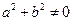 且
且 .设
.设 .
. ,
,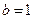 ,
,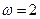 ,求方程
,求方程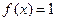 在区间
在区间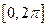 内的解集;
内的解集;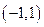 且法向量为
且法向量为 的直线
的直线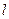 上的动点.当
上的动点.当 时,设函数
时,设函数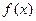 的值域为集合
的值域为集合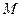 ,不等式
,不等式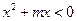 的解集为集合
的解集为集合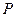 . 若
. 若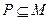 恒成立,求实数
恒成立,求实数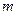 的最大值;
的最大值;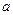 、
、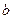 和
和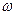 的值. 当
的值. 当 对称,且在
对称,且在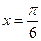 处
处 中,
中,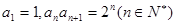
 项和
项和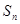 ;
;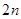 项和为
项和为 ,若
,若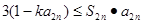 对任意
对任意 恒成立,求
恒成立,求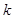 的最小值.
的最小值.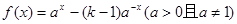 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;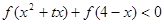 恒成立的
恒成立的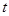 的取值范围;
的取值范围;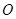 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为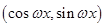 ,其中
,其中 且
且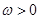 .设
.设 .
.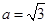 ,
, ,
, ,求方程
,求方程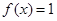 在区间
在区间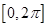 内的解集;
内的解集;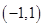 且法向量为
且法向量为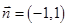 的直线
的直线 上的动点.当
上的动点.当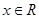 时,设函数
时,设函数 的值域为集合
的值域为集合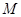 ,不等式
,不等式 的解集为集合
的解集为集合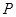 . 若
. 若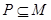 恒成立,求实数
恒成立,求实数 的最大值;
的最大值;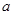 、
、 和
和 的值. 当
的值. 当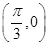 对称,且在
对称,且在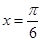 处
处