题目内容
圆C：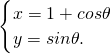
（θ为参数）的圆心坐标是________；若直线ax+y+1=0与圆C相切，则a的值为________．
（1，0） 0
分析：把圆的参数方程化为圆的标准方程，找出圆心坐标和半径r，然后利用点到直线的距离公式求出圆心到已知直线的距离d，让d等于r列出关于a的方程，即可求出a的值．
解答：把圆的参数方程化为普通方程得：（x-1）2+y2=1，
∴圆心坐标为（1，0），半径r=1，
圆心到直线ax+y+1=0的距离d=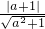
=r=1，
化简得：（a+1）2=a2+1，即2a=0，解得：a=0．
故答案为：（1，0）；0
点评：本小题主要考查圆的参数方程及直线与圆的位置关系的判断，以及转化与化归的思想方法．本题出现最多的问题应该是计算上的问题，平时要强化基本功的练习．
分析：把圆的参数方程化为圆的标准方程，找出圆心坐标和半径r，然后利用点到直线的距离公式求出圆心到已知直线的距离d，让d等于r列出关于a的方程，即可求出a的值．
解答：把圆的参数方程化为普通方程得：（x-1）2+y2=1，
∴圆心坐标为（1，0），半径r=1，
圆心到直线ax+y+1=0的距离d=
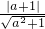=r=1，化简得：（a+1）2=a2+1，即2a=0，解得：a=0．
故答案为：（1，0）；0
点评：本小题主要考查圆的参数方程及直线与圆的位置关系的判断，以及转化与化归的思想方法．本题出现最多的问题应该是计算上的问题，平时要强化基本功的练习．
练习册系列答案
相关题目