Question

已知平面直角坐标系中，A₁(-2，0)，A₂(2,0)、A₃(1,)，△A₁A₂A₃的外接圆为C；椭圆C₁以线段A₁A₂为长轴，离心率e=.

（1）求圆C及椭圆C₁的方程；

（2）设椭圆C₁的右焦点为F，点P为圆C上异于A₁、A₂的动点，过原点O作直线PF的垂线交直线x=2于点Q，判断直线PQ与圆C的位置关系，并给出证明.

Answer 1

解:（1）∵|OA₁|=|OA₂|=|OA₃|=2,

∴外接圆C以原点O为圆心,线段OA₁为半径.故其方程为x²+y²=4.

∴2a=4.∴a=2.又e=,∴c=,可得b=.

∴所求椭圆C₁的方程是+=1.

（2）直线PQ与圆C相切.证明：设P(x₀,y₀)(x₀≠±2),则y₀²=4-x₀².

当x₀=时,P(,±),Q(2,0),k_OP·k_PQ=-1,∴OP⊥PQ;

当x₀≠2时,k_PF=,∴k_OQ=.∴直线OQ的方程为y=x.

因此,点Q的坐标为(2,).

∵k_PQ==,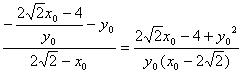

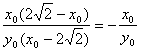∴当x₀=0时,k_PQ=0,OP⊥PQ;当x₀≠0时,k_OP=,

∴k_PQ·k_OP=-1,OP⊥PQ.综上,当x≠±2时,OP⊥PQ,故直线PQ始终与圆C相切.