Question

【题目】已知且,设:函数在上单调递减, :函数的图象与轴交于不同的两点.如果真, 假,求实数的取值范围.

Answer 1

【答案】

【解析】

试题分析：根据对数函数的单调性我们易判断出命题p为真命题时参数a的取值范围，及命题p为假命题时参数a的取值范围；根据二次函数零点个数的确定方法，我们易判断出命题q为真命题时参数a的取值范围，及命题q为假命题时参数a的取值范围；由p且q为假命题，p或q为真命题，我们易得到p与q一真一假，分类讨论，分别构造关于x的不等式组，解不等式组即可得到答案．

详解：若p为真，则0＜a＜1．若q为真，

则△＞0即（2a﹣3）2﹣4＞0解得a＜或a＞．

∵p且q为假，p或q为真，

∴p与q中有且只有一个为真命题．（a＞0且a≠1）

若p真q假，则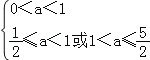

∴≤a＜1

若p假q真，则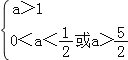

∴a

综上所述，a的取值范围为：[，1）∪（，+∞）．