题目内容
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线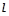 经过点P(1,1),倾斜角
经过点P(1,1),倾斜角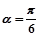 .
.
(1)写出直线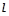 的参数方程;
的参数方程;
(2)设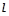 与圆
与圆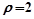 相交于两点A、B,求点P到A、B两点的距离之积.
相交于两点A、B,求点P到A、B两点的距离之积.
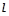 经过点P(1,1),倾斜角
经过点P(1,1),倾斜角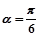 .
.(1)写出直线
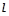 的参数方程;
的参数方程; (2)设
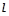 与圆
与圆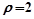 相交于两点A、B,求点P到A、B两点的距离之积.
相交于两点A、B,求点P到A、B两点的距离之积.(1) (2)2
(2)2
 (2)2
(2)2本题考查了直线的参数方程、简单曲线的极坐标方程和直线与圆的位置关系等知识点,属于中档题.请同学们注意解题过程中用根与系数的关系,设而不求的思想方法.
(I)设出直线l上任意一点Q,利用直线斜率的坐标公式可得到坐标的关系:(y-1):(x-1)=1: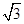 ,再令x-1=
,再令x-1=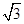 t,以t为参数,可以得到直线l的参数方程;
t,以t为参数,可以得到直线l的参数方程;
(II)将圆ρ=2化成普通方程,再与直线的参数方程联解,得到一个关于t的一元二次方程.再用一元二次方程根与系数的关系,结合两点的距离公式,可得出P到A、B两点的距离之积.
解:(I)直线的参数方程是
 ---5分
---5分
(II)因为点A,B都在直线l上,所以可设它们对应的参数为t1和t2,则点A,B的坐标分别为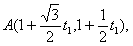
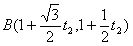 .
.
圆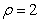 化为直角坐标系的方程
化为直角坐标系的方程 .
.
以直线l的参数方程代入圆的方程 整理得到
整理得到
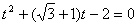 ①
①
因为t1和t2是方程①的解,从而t1t2=-2.
所以|PA|·|PB|= |t1t2|=|-2|=2. -----------------(12分)
(I)设出直线l上任意一点Q,利用直线斜率的坐标公式可得到坐标的关系:(y-1):(x-1)=1:
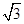 ,再令x-1=
,再令x-1=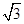 t,以t为参数,可以得到直线l的参数方程;
t,以t为参数,可以得到直线l的参数方程;(II)将圆ρ=2化成普通方程,再与直线的参数方程联解,得到一个关于t的一元二次方程.再用一元二次方程根与系数的关系,结合两点的距离公式,可得出P到A、B两点的距离之积.
解:(I)直线的参数方程是
 ---5分
---5分(II)因为点A,B都在直线l上,所以可设它们对应的参数为t1和t2,则点A,B的坐标分别为
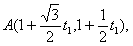
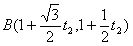 .
.圆
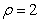 化为直角坐标系的方程
化为直角坐标系的方程 .
.以直线l的参数方程代入圆的方程
 整理得到
整理得到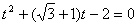 ①
①因为t1和t2是方程①的解,从而t1t2=-2.
所以|PA|·|PB|= |t1t2|=|-2|=2. -----------------(12分)

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
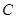 :
: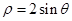 的圆心到直线
的圆心到直线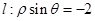 的距离为_________ .
的距离为_________ .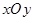 中,圆
中,圆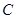 的参数方程为
的参数方程为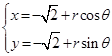
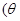 为参数,
为参数,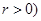 .以
.以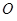 为极点,
为极点,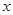 轴正半轴为极轴,并取相同的单位长度建立极坐标系,直线
轴正半轴为极轴,并取相同的单位长度建立极坐标系,直线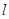 的极坐标方程为
的极坐标方程为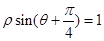 .当圆
.当圆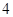 时,圆的半径
时,圆的半径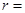 .
.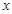 轴的正半轴为极轴建坐标系,已知曲线
轴的正半轴为极轴建坐标系,已知曲线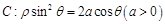 ,已知过点
,已知过点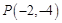 的直线
的直线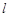 的参数方程为:
的参数方程为: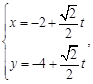 直线
直线 分别交于
分别交于
 和直线
和直线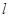 的普通方程;
的普通方程;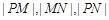 成等比数列,求
成等比数列,求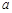 的值.
的值. 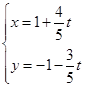 (
(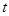 为参数)被曲线
为参数)被曲线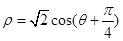 所截的弦长.
所截的弦长.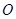 为极点,
为极点,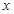 轴的非负半轴为极轴建立极坐标系. 已知点
轴的非负半轴为极轴建立极坐标系. 已知点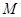 的极坐标为
的极坐标为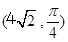 ,曲线
,曲线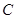 的参数方程为
的参数方程为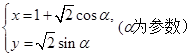 .
.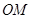 的直角坐标方程;
的直角坐标方程;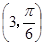 ,半径
,半径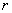 =1,Q点在圆C上运动。
=1,Q点在圆C上运动。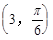 ,半径为3的圆的极坐标方程。
,半径为3的圆的极坐标方程。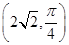 作圆
作圆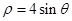 的切线,则切线的极坐标方程是 .
的切线,则切线的极坐标方程是 .