题目内容
4.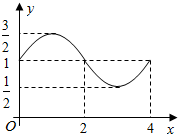 如图所示,函数 f(x)=Asin(ωx+φ)+B的图象,则S=f(1)+f(2)+f(3)+…+f(2015)=2015.
如图所示,函数 f(x)=Asin(ωx+φ)+B的图象,则S=f(1)+f(2)+f(3)+…+f(2015)=2015.
分析 由函数的图象的顶点坐标求出A、B,由周期求出ω,由特殊点的坐标求出φ的值,可得函数的解析式,再利用函数的周期性求得所给式子的值.
解答 解:由函数 f(x)=Asin(ωx+φ)+B的图象,可得B=1,A=$\frac{3}{2}$-1=$\frac{1}{2}$,
周期为T=4=$\frac{2π}{ω}$,求得ω=$\frac{π}{2}$.
再把点(0,1)代入,可得$\frac{1}{2}$sinφ+1=1,可得sinφ=0,故可取φ=0,f(x)=$\frac{1}{2}$sin($\frac{π}{2}$x)+1,
f(1)+f(2)+f(3)+f(4)=$\frac{3}{2}$+1+$\frac{1}{2}$+1=4,
S=f(1)+f(2)+f(3)+…+f(2015)=503×[f(1)+f(2)+f(3)+f(4)]+f(1)+f(2)+f(3)
=503×4+$\frac{3}{2}$+1+$\frac{1}{2}$=2015,
故答案为:2015.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A、B,由周期求出ω,由特殊点的坐标求出φ的值,函数的周期性的应用,属于中档题.

练习册系列答案
相关题目
9.已知函数y=f(x+1)定义域是[-2,1],则y=f(2x-1)的定义域( )
| A. | [0,$\frac{3}{2}$] | B. | [-1,4] | C. | [-5,5] | D. | [-3,7] |
16.已知命题p:?x0∈(-∞,0),2${\;}^{{x}_{0}}$<1,命题q:?x∈R,x+$\frac{1}{x}$≥2,则( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是真命题 | D. | 命题p∨(¬q)是假命题 |