题目内容
14．已知抛物线方程为y2=4x，焦点坐标为F，点P在抛物线上且|PF|=4，圆的方程为（x+2）2+y2=1，过点P作圆的切线，则切线长为6．分析 先求出P的坐标，再利用勾股定理求出切线长．
解答 解：抛物线方程为y2=4x，准线方程为x=-1，
∵点P在抛物线上且|PF|=4，
∴P的横坐标为3，
∴P（3，±2$\sqrt{3}$），
∵圆心为C（-2，0），半径为1，
∴|CP|=$\sqrt{25+12}$=$\sqrt{37}$，
∴切线长为$\sqrt{37-1}$=6，
故答案为：6．
点评 本题考查抛物线的方程与性质，考查直线与圆的位置关系，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
9．
某单位N名员工参加“社区低碳你我他”活动，他们的年龄在25岁至50岁之间，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如图所示，下表是年龄的频率分布表．
（1）求正整数a，b，N的值；
（2）现要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，则年龄在第1，2，3组的人数分别是多少？
（3）在（2）的条件下，从这6人中随机抽取2人参加社区宣传交流活动，求恰有1人在第3组的概率．
某单位N名员工参加“社区低碳你我他”活动，他们的年龄在25岁至50岁之间，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如图所示，下表是年龄的频率分布表．| 区间 | [25，30） | [30，35） | [35.40） | [40，45） | [45，50） |
| 人数 | 25 | a | b |
（2）现要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，则年龄在第1，2，3组的人数分别是多少？
（3）在（2）的条件下，从这6人中随机抽取2人参加社区宣传交流活动，求恰有1人在第3组的概率．
6．执行如图所示的程序框图，则输出Sn=（ ）
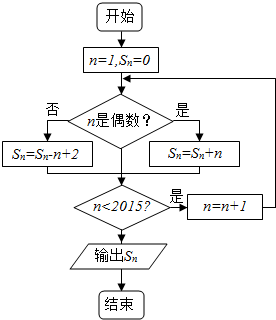
| A． | 0 | B． | 2 | C． | 1008 | D． | 3021 |
如图所示，函数 f（x）=Asin（ωx+φ）+B的图象，则S=f（1）+f（2）+f（3）+…+f（2015）=2015．