题目内容
【题目】已知椭圆![]() 的方程是
的方程是![]() ,双曲线
,双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() 的左右顶点,而
的左右顶点,而![]() 的左右顶点分别是
的左右顶点分别是![]() 的左右焦点.
的左右焦点.
(1)求双曲线![]() 的方程;
的方程;
(2)若直线![]() 与双曲线
与双曲线![]() 恒有两个不同的交点,且
恒有两个不同的交点,且![]() 与
与![]() 的两个交点A和B满足
的两个交点A和B满足![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)求出椭圆的焦点即为双曲线的顶点,椭圆的顶点即为双曲线的焦点,即有a=![]() ,c=2,b=1.即可得到双曲线方程;
,c=2,b=1.即可得到双曲线方程;
(2)联立直线方程和双曲线方程,消去y,得到x的方程,运用韦达定理和判别式大于0,再由向量的数量积的坐标运算,化简和整理得到k的不等式,解出求它们的交集即可.
试题解析:
(1)椭圆C1的方程为![]() 的左、右焦点为(﹣
的左、右焦点为(﹣![]() ,0),(
,0),(![]() ,0),
,0),
则C2的左、右顶点为(﹣![]() ,0),(
,0),(![]() ,0),C1的左、右顶点为(﹣2,0),(2,0),则C2的左、右焦点为(﹣2,0),(2,0).则双曲线的a=
,0),C1的左、右顶点为(﹣2,0),(2,0),则C2的左、右焦点为(﹣2,0),(2,0).则双曲线的a=![]() ,c=2,b=1.
,c=2,b=1.
即有双曲线C2的方程为: ![]() ;
;
(2)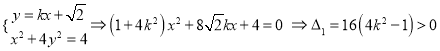 ①
①
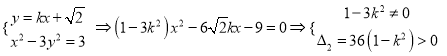 ②
②
由①②得![]() ,
,![]() ③
③
由①②③得![]()

 快捷英语周周练系列答案
快捷英语周周练系列答案【题目】已知幂函数f(x)=x﹣m2+m+2(m∈Z)在(0,+∞)上单调递增.
(1)求函数f(x)的解析式;
(2)设g(x)=f(x)﹣ax+1,a为实常数,求g(x)在区间[﹣1,1]上的最小值.
【题目】(2017·全国卷Ⅲ文,18)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算电费.每月用电不超过100度时,按每度0.57元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(1)设月用电x度时,应交电费y元,写出y关于x的函数关系式;
(2)小明家第一季度缴纳电费情况如下:问小明家第一季度共用电多少度?
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
【题目】某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4, 则该产品为一等品.先从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标 (x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标 (x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样本的一等品中, 随机抽取2件产品,
(ⅰ) 用产品编号列出所有可能的结果;
(ⅱ) 设事件B为“在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.
