题目内容
(本小题满分16分) 已知函数
 ,在
,在 处的
处的
切线方程为 .
.
(1)求 的解析式;
的解析式;
(2)设
 ,若对任意
,若对任意 ,总存在
,总存在 ,使得
,使得
 成立,求实数
成立,求实数 的取值范围.
的取值范围.

 ,在
,在 处的
处的切线方程为
 .
.(1)求
 的解析式;
的解析式;(2)设

 ,若对任意
,若对任意 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.解:(1)将 带入切线方程可得切点为
带入切线方程可得切点为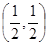 。
。
所以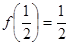 ,即
,即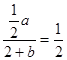 ①…………………………………(2分)
①…………………………………(2分)
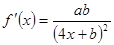
由导数的几何意义得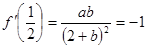 ②…………………(4分)
②…………………(4分)
联立①②,解之得:
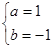 ,所以
,所以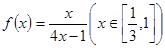 。……………………(7分)
。……………………(7分)
(2)由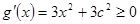 ,知
,知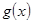 在
在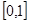 上是增函数。则
上是增函数。则
 .
.
故函数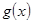 在值域为
在值域为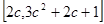 。……………………(9分)
。……………………(9分)
因为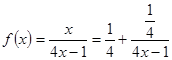 在
在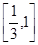 上是减函数,所以,
上是减函数,所以,
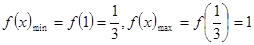 。……………………(12分)
。……………………(12分)
故函数 的值域为
的值域为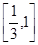 。
。
由题设得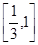 Í
Í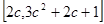 。
。
则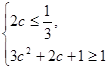
解得 的取值范围为
的取值范围为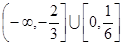 。……………………(16分)
。……………………(16分)
 带入切线方程可得切点为
带入切线方程可得切点为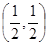 。
。所以
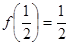 ,即
,即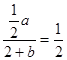 ①…………………………………(2分)
①…………………………………(2分)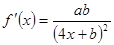
由导数的几何意义得
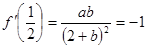 ②…………………(4分)
②…………………(4分)联立①②,解之得:
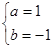 ,所以
,所以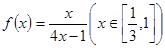 。……………………(7分)
。……………………(7分)(2)由
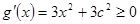 ,知
,知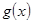 在
在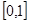 上是增函数。则
上是增函数。则 .
.故函数
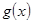 在值域为
在值域为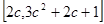 。……………………(9分)
。……………………(9分)因为
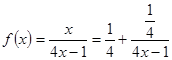 在
在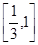 上是减函数,所以,
上是减函数,所以,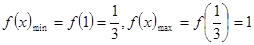 。……………………(12分)
。……………………(12分)故函数
 的值域为
的值域为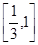 。
。由题设得
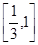 Í
Í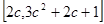 。
。则
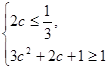
解得
 的取值范围为
的取值范围为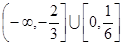 。……………………(16分)
。……………………(16分)略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的定义域为D,若
的定义域为D,若 满足下面两个条件,则称
满足下面两个条件,则称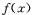 为闭函数.①
为闭函数.① 在D内是单调函数;②存在
在D内是单调函数;②存在 ,使f(x)在[a,b]上的值域为[a,b].如果
,使f(x)在[a,b]上的值域为[a,b].如果 为闭函数,那么k的取值范围是
为闭函数,那么k的取值范围是
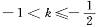
 ),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
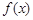 的定义域为
的定义域为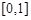 ,且同时满足:①
,且同时满足:①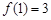 ;②
;②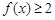 恒成立;③若
恒成立;③若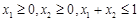 ,则有
,则有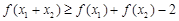 .
.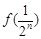 与
与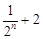 的大小
的大小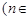 N);
N);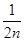 (nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1
(nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1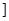 ,都有
,都有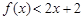 ,请你判断此猜想是否正确,并说明理由.
,请你判断此猜想是否正确,并说明理由. 的图象在点
的图象在点 处的切线方程是
处的切线方程是 ,则
,则 ____.
____. ,且
,且 ,则
,则 ( )
( )
 中,函数
中,函数 (
( )的图像与
)的图像与 轴交于点
轴交于点 ,它的反函数
,它的反函数 的图像与
的图像与 轴交于点
轴交于点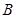 ,并且这两个函数的图像交于点
,并且这两个函数的图像交于点 .若四边形
.若四边形 的面积是
的面积是 ,则
,则 ___________.
___________. ,那么
,那么 =________.
=________.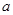 <b+1,且
<b+1,且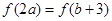 ,则T=3a2+b的取值范围
,则T=3a2+b的取值范围 ,+∞)
,+∞) ,0)
,0)  )
) ,0)
,0)