题目内容
【题目】如图下图①,等边三角形ABC的边长为2a,CD是AB边上的高,E,F分别是AC和BC边上的点,且满足![]() =k,现将△ABC沿CD翻折成直二面角ADCB,如图下图②.
=k,现将△ABC沿CD翻折成直二面角ADCB,如图下图②.
(1)试判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角BACD的正切值.
① ②
②
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)根据AB平行EF即可说明(2)过点D作DG⊥AC于点G,连接BG,可证∠BGD是二面角BACD的平面角,解三角形即可求出.
(1)AB∥平面DEF,
理由如下:在△ABC中,
因为E,F分别是AC,BC上的点,且满足![]() =
=![]() =k,
=k,
所以AB∥EF.
因为AB平面DEF,EF平面DEF,
所以AB∥平面DEF.
(2)如图所示,过点D作DG⊥AC于点G,连接BG.
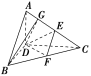
因为AD⊥CD,BD⊥CD,
所以∠ADB是二面角ACDB的平面角.
所以∠ADB=90°,即BD⊥AD.
所以BD⊥平面ADC.
所以BD⊥AC.
所以AC⊥平面BGD.
所以BG⊥AC.
所以∠BGD是二面角BACD的平面角.
在△ADC中,AD=a,DC=![]() a,AC=2a,所以DG=
a,AC=2a,所以DG=![]() =
=![]() =
=![]() .
.
在Rt△BDG中,tan∠BGD=![]() =
=![]() ,即二面角BACD的正切值为
,即二面角BACD的正切值为![]() .
.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】某综艺节目为增强娱乐性,要求现场嘉宾与其场外好友连线互动.凡是拒绝表演节目的好友均无连线好友的机会;凡是选择表演节目的好友均需连线未参加过此活动的3个好友参与此活动,以此下去.
(Ⅰ)假设每个人选择表演与否是等可能的,且互不影响,则某人选择表演后,其连线的3个好友中不少于2个好友选择表演节目的概率是多少?
(Ⅱ)为调查“选择表演者”与其性别是否有关,采取随机抽样得到如表:
选择表演 | 拒绝表演 | 合计 | |
男 | 50 | 10 | 60 |
女 | 10 | 10 | 20 |
合计 | 60 | 20 | 80 |
①根据表中数据,是否有99%的把握认为“表演节目”与好友的性别有关?
②将此样本的频率视为总体的概率,随机调查3名男性好友,设X为3个人中选择表演的人数,求X的分布列和期望.
附:K2= ![]() ;
;
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |