题目内容
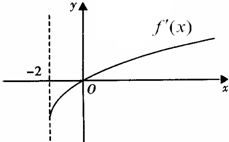 已知:函数f(x)的定义域为[-2,+∞),且f(4)=f(-2)=1,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,则
已知:函数f(x)的定义域为[-2,+∞),且f(4)=f(-2)=1,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,则
|
| A、2 | B、4 | C、5 | D、8 |
分析:利用导函数的图象判断出函数的单调性;利用函数的单调性化简不等式f(2a+b)≤1;画出不等式组表示的平面区域;利用三角形的面积公式求出区域的面积.
解答:解:由导函数的图象得到f(x)在[-2,0]递减;在[0,+∞)递增
∵f(4)=f(-2)=1
∴f(2a+b)≤1?-2≤2a+b≤4
∴
?
表示的平面区域如下
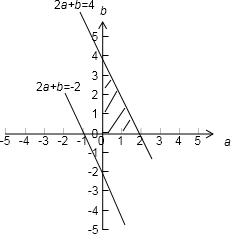
所以平面区域的面积为
×2×4=4
故选B
∵f(4)=f(-2)=1
∴f(2a+b)≤1?-2≤2a+b≤4
∴
|
|

所以平面区域的面积为
| 1 |
| 2 |
故选B
点评:本题考查函数的单调性与导函数符号的关系、考查利用函数的单调性求抽象不等式、考查如何画不等式组表示的平面区域.

练习册系列答案
相关题目
已知奇函数f(x)的定义域为(-∞,0)∪(0,+∞),且对任意正实数x1、x2(x1≠x2),恒
有
>0,则一定有( )
有
| f(x1)-f(x2) |
| x1-x2 |
A、f(cos600°)>f(log
| |||||
B、f(cos600°)>f(-log
| |||||
C、f(-cos600°)>f(log
| |||||
D、f(-cos600°)>f(-log
|