题目内容
10.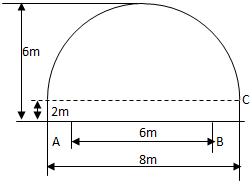 如图,一隧道由一个长方形和抛物线构成,现欲在隧道抛物线拱顶上安装交通信息采集装置,若位置C对隧道底AB的张角最大时采集效果最好,则采集效果最好时位置C到AB的距离是6-$\sqrt{15}$.
如图,一隧道由一个长方形和抛物线构成,现欲在隧道抛物线拱顶上安装交通信息采集装置,若位置C对隧道底AB的张角最大时采集效果最好,则采集效果最好时位置C到AB的距离是6-$\sqrt{15}$.
分析 建立如图所示的坐标系,求出抛物线的方程,设C(x,y)(y>-6),由A(-3,-6),B(3,-6),可得kCA=$\frac{y+6}{x+3}$,kCB=$\frac{y+6}{x-3}$,可得tan∠BCA,利用基本不等式,即可得出结论.
解答  解:建立如图所示的坐标系,设抛物线方程为x2=-2py(p>0),
解:建立如图所示的坐标系,设抛物线方程为x2=-2py(p>0),
将点(4,-4)代入,可得p=2,
所以抛物线方程为x2=-4y,
设C(x,y)(y>-6),则
由A(-3,-6),B(3,-6),可得kCA=$\frac{y+6}{x+3}$,kCB=$\frac{y+6}{x-3}$,
∴tan∠BCA=$\frac{\frac{y+6}{x+3}-\frac{y+6}{x-3}}{1+\frac{y+6}{x+3}•\frac{y+6}{x-3}}$=$\frac{-6(y+6)}{{x}^{2}-9+(y+6)^{2}}$
=$\frac{-6(y+6)}{{y}^{2}+8y+27}$,
令t=y+6(t>0),则tan∠BCA=$\frac{-6t}{{t}^{2}-4t+15}$=$\frac{-6}{t+\frac{15}{t}-4}$≤$\frac{-6}{2\sqrt{15}-4}$,
所以t=$\sqrt{15}$,y=$\sqrt{15}$-6时,位置C对隧道底AB的张角最大,
故答案为:6-$\sqrt{15}$.
点评 本题考查抛物线的方程与应用,考查基本不等式,确定抛物线的方程及tan∠BCA,正确运用基本不等式是关键.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
2.已知tanx=2,则tan2(x-$\frac{π}{4}$)等于( )
| A. | $\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |