题目内容
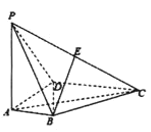
【题目】如图, 在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
,![]() ,
, ![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
(1)证明:![]() :
:
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)若![]() 为棱
为棱![]() 上一点, 满足
上一点, 满足![]() , 求二面角
, 求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析 (2)![]() (3)
(3)![]()
【解析】
(1)根据题意以![]() 为坐标原点,建立空间直角坐标系,写出各个点的坐标,并表示出
为坐标原点,建立空间直角坐标系,写出各个点的坐标,并表示出![]() ,由空间向量数量积运算即可证明
,由空间向量数量积运算即可证明![]() .
.
(2)先求得平面![]() 的法向量,即可求得直线
的法向量,即可求得直线![]() 与平面法向量夹角的余弦值,即为直线
与平面法向量夹角的余弦值,即为直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)由![]() 点在棱
点在棱![]() 上,设
上,设![]() ,再由
,再由![]() ,结合
,结合![]() ,由空间向量垂直的坐标关系求得
,由空间向量垂直的坐标关系求得![]() 的值.即可表示出
的值.即可表示出![]() .求得平面
.求得平面![]() 和平面
和平面![]() 的法向量,由空间向量数量积的运算求得两个平面夹角的余弦值,再根据二面角的平面角为锐角即可确定二面角
的法向量,由空间向量数量积的运算求得两个平面夹角的余弦值,再根据二面角的平面角为锐角即可确定二面角![]() 的余弦值.
的余弦值.
(1)证明:∵![]() 底面
底面![]() ,
,![]() ,
,
以![]() 为坐标原点,建立如图所示的空间直角坐标系,
为坐标原点,建立如图所示的空间直角坐标系,

∵![]() ,
,![]() ,点
,点![]() 为棱
为棱 ![]() 的中点.
的中点.
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(2)![]() ,
,
设平面![]() 的法向量为
的法向量为![]() .
.
则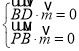 ,代入可得
,代入可得![]() ,
,
令![]() 解得
解得![]() ,即
,即![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,由直线与平面夹角可知
,由直线与平面夹角可知

所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(3)![]() ,
,
由![]() 点在棱
点在棱![]() 上,设
上,设![]() ,
,
故![]() ,
,
由![]() ,得
,得![]() ,
,
解得![]() ,
,
即![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由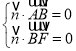 ,得
,得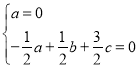 ,
,
令![]() ,则
,则![]()
取平面![]() 的法向量
的法向量![]() ,
,
则二面角![]() 的平面角
的平面角![]() 满足
满足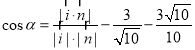 ,
,
由图可知,二面角![]() 为锐二面角,
为锐二面角,
故二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】某度假酒店为了解会员对酒店的满意度,从中抽取50名会员进行调查,把会员对酒店的“住宿满意度”与“餐饮满意度”都分别五个评分标准:1分(很不满意);2分(不满意);3分(一般);4分(满意);5分(很满意),其统计结果如下表(住宿满意度为x,餐饮满意度为y).
餐饮满意度y 人数 住宿满意度x | 1 | 2 | 3 | 4 | 5 |
1 | 1 | 1 | 2 | 1 | 0 |
2 | 2 | 1 | 3 | 2 | 1 |
3 | 1 | 2 | 5 | 3 | 4 |
4 | 0 | 3 | 5 | 4 | 3 |
5 | 0 | 0 | 1 | 2 | 3 |
(1)求“住宿满意度”分数的平均数;
(2)求“住宿满意度”为3分时的5个“餐饮满意度”人数的方差;
(3)为提高对酒店的满意度,现从![]() 且
且![]() 的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.