题目内容
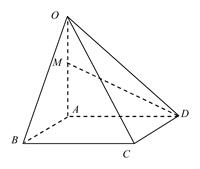
(本小题满分10分)如图,在四棱锥OABCD中,底面ABCD是边长为1的菱形,∠ABC=45°,OA⊥底面ABCD,OA=2,M为OA的中点.
(1) 求异面直线AB与MD所成角的大小;
(2) 求平面OAB与平面OCD所成二面角的余弦值.
(1) 求异面直线AB与MD所成角的大小;
(2) 求平面OAB与平面OCD所成二面角的余弦值.

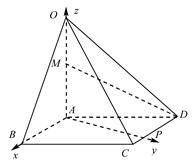
作AP⊥CD于点P,分别以AB、AP、AO所在直线为x、y、z轴建立坐标系,则A(0,0,0),B(1,0,0),
P,D,O(0,0,2),M(0,0,1).
(1) =(1,0,0),=,
则cos〈,〉=-,
故AB与MD所成角为.(4分)
 (2) =,=,
(2) =,=,
设平面OCD的法向量n=(x,y,z ),
),
则n·=0,n·=0,
即
取z=,则n=(0,4,).(6分)
易得平面OAB的一个法向量为m=(0,1,0),
cos〈n,m〉=,(9分)
故平面OAB与平面OCD所成二面角的平面角余弦值为.(10分)
P,D,O(0,0,2),M(0,0,1).
(1) =(1,0,0),=,
则cos〈,〉=-,
故AB与MD所成角为.(4分)
 (2) =,=,
(2) =,=,设平面OCD的法向量n=(x,y,z
 ),
),则n·=0,n·=0,
即
取z=,则n=(0,4,).(6分)
易得平面OAB的一个法向量为m=(0,1,0),
cos〈n,m〉=,(9分)
故平面OAB与平面OCD所成二面角的平面角余弦值为.(10分)
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,E、F分别是AB、CD的中点,EF=
,E、F分别是AB、CD的中点,EF=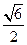 求异面直线AD和BC所成的角。
求异面直线AD和BC所成的角。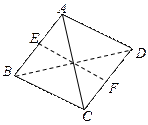
 B
B 分别为棱AC、AB上的动点(不包括端点),若
分别为棱AC、AB上的动点(不包括端点),若

 则线段DE长度的取值范围为
则线段DE长度的取值范围为 B.
B. C.
C. D.
D.
 B
B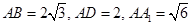 ,则点
,则点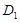 到直线AC的距离是
到直线AC的距离是 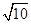
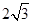
 垂直于矩形
垂直于矩形 所在的平面,
所在的平面,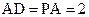 ,
, ,
, 、
、 分别是
分别是 、
、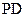 的中点.
的中点.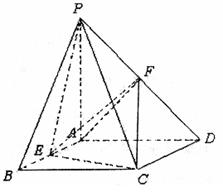
 平面
平面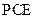 ;
; 平面
平面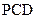 ;
; 的体积
的体积 的外接球球心在
的外接球球心在 上,且
上,且 ,
, ,在外接球面上
,在外接球面上 两点
两点 间的球面距离是 。
间的球面距离是 。
 3个
3个