题目内容
在空间四边形ABCD中,AD=BC=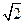 ,E、F分别是AB、CD的中点,EF=
,E、F分别是AB、CD的中点,EF=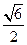 求异面直线AD和BC所成的角。
求异面直线AD和BC所成的角。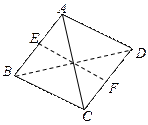
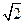 ,E、F分别是AB、CD的中点,EF=
,E、F分别是AB、CD的中点,EF=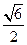 求异面直线AD和BC所成的角。
求异面直线AD和BC所成的角。
解:取AC中点G联接EG、FG,则EG、FG分别是△ABC、△ADC中位线
∴EG//BC、FG//AD
∴∠EGF是异面直线AD和BC所成的角或者其补角
在△EFG中,EG= BC=
BC=
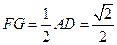 EF=
EF=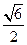
在△EFG中由余弦定理知: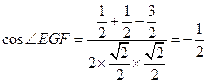
∴∠EGF=1200 ∴异面直线AD和BC所成的角为600
(1)解:(1)
 .
.
由余弦定理:
整理得: ∴
∴ ∴△ABC为直角三角形
∴△ABC为直角三角形
∴EG//BC、FG//AD
∴∠EGF是异面直线AD和BC所成的角或者其补角
在△EFG中,EG=
 BC=
BC=
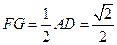 EF=
EF=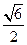
在△EFG中由余弦定理知:
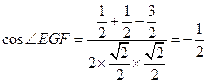
∴∠EGF=1200 ∴异面直线AD和BC所成的角为600
(1)解:(1)

 .
.由余弦定理:

整理得:
 ∴
∴ ∴△ABC为直角三角形
∴△ABC为直角三角形略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
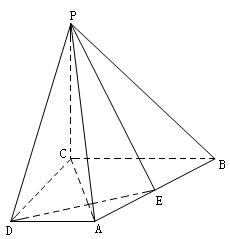
 中,
中,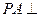 底面
底面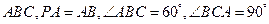 ,点
,点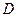 ,
,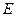 分别在棱
分别在棱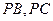 上,且
上,且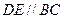
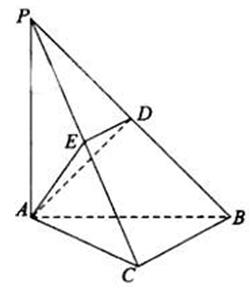
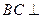 平面
平面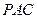 ;
;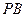 的中点时,求
的中点时,求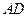 与平面
与平面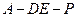 为直二面角?并说明理由.
为直二面角?并说明理由.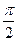 ,
,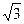 ;
;

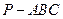 中,
中,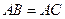 ,
, 为
为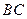 的
的 中点,
中点,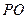 ⊥平面
⊥平面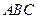 ,垂足
,垂足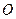 落在线段
落在线段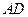 上.
上.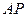 ⊥
⊥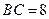 ,
,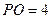 ,
,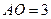 ,
, .求二面角
.求二面角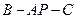 的大小.
的大小.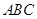 中,
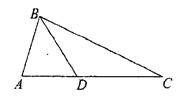
中,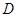 是边
是边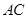 上的点,且
上的点,且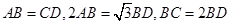 ,
,
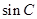 的值为( )A.
的值为( )A.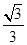 B.
B.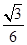
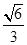 D.
D.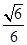
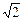 。
。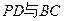 所成的角;(3)求四棱锥P-ABCD的体积。
所成的角;(3)求四棱锥P-ABCD的体积。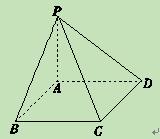
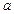 ,点D,E分别是边OA,BC的中点,连结DE
,点D,E分别是边OA,BC的中点,连结DE
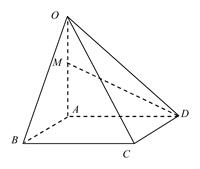
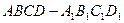 的下底面
的下底面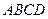 是边长为
是边长为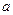 的正方形,
的正方形,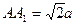 ,且点
,且点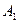 在下底面
在下底面
 点.
点.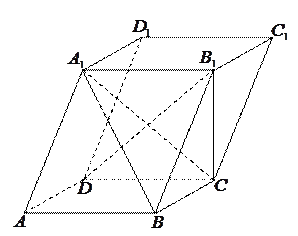
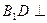 面
面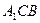 ;
;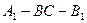 的大小.
的大小.