题目内容
平面直角坐标系中,点集M=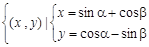
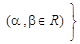 ,则点集M所覆盖的平面图形的面积为
,则点集M所覆盖的平面图形的面积为
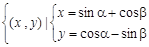
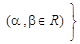 ,则点集M所覆盖的平面图形的面积为
,则点集M所覆盖的平面图形的面积为 A. | B. | C. | D.与 有关 有关 |
A
分析:欲求点集M所覆盖的平面图形的面积,先看点M的轨迹是什么图形才行,将x,y的式子平方相加后即可得出x2+y2=2+2sin(α-β).再结合三角函数的有界性即可解决问题.
解:∵
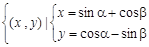
两式平方相加得:
x2+y2=1+1+2sinαcosβ-2cosαsinβ
即:x2+y2=2+2sin(α-β).
由于-1≤sin(α-β)≤1,
∴0≤2+2sin(α-β)≤4,
∴随着α-β 的变化,方程x2+y2=2+2sin(α-β)圆心在(0,0),半径最大为2的圆,
点集M所覆盖的平面图形的面积为:2×2×π=4π.
故选A.

练习册系列答案
相关题目
 系
系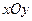 中,以
中,以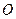 为极点,
为极点,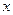 正半轴为极轴建立极坐标系,曲线
正半轴为极轴建立极坐标系,曲线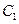 的极坐标方程为
的极坐标方程为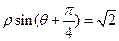 ,
, 分别为
分别为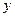 轴的交点。曲线
轴的交点。曲线 的参数方程为
的参数方程为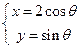 (
(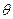 为参数)。
为参数)。 方程;
方程;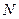 点与曲线
点与曲线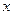 轴的正半轴重合,曲线
轴的正半轴重合,曲线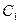 :
: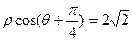 与曲线
与曲线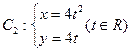 交于A、B两点。
交于A、B两点。 化成普通方程是_______________
化成普通方程是_______________ 为参数,
为参数, 上一点,直线
上一点,直线 的倾斜角
的倾斜角 ,O为坐标原点,则点
,O为坐标原点,则点 的坐标是__________。
的坐标是__________。 (本小题满分10分)选修4-4:坐标系统与参数方程
(本小题满分10分)选修4-4:坐标系统与参数方程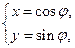 (
(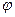 为参数)曲线C2的参数方程为
为参数)曲线C2的参数方程为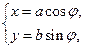 (
(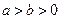 ,
,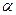 与C1,C2各
与C1,C2各 有一个交点.当
有一个交点.当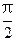 时,这两个交点重合。
时,这两个交点重合。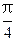 时,l与C1,C2的交点分别为A1,B1,当
时,l与C1,C2的交点分别为A1,B1,当 2,求四边形A1A2B2B1的面积。
2,求四边形A1A2B2B1的面积。
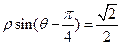 与圆
与圆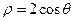 的位置关系是 。
的位置关系是 。 ,不等式
,不等式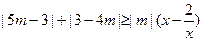 恒成立,则实数
恒成立,则实数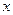 的取值范围是 。
的取值范围是 。 为曲线
为曲线 的切线,且与直线
的切线,且与直线
 垂直.
垂直. 由直线
由直线 、
、 和
和 轴所围成的三角形
轴所围成的三角形 的面积.
的面积.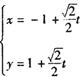 (r为参数),曲线C的极坐标方程是
(r为参数),曲线C的极坐标方程是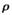 =2,直线l与曲线C交于A、B,则|AB| ="(" )
=2,直线l与曲线C交于A、B,则|AB| ="(" )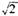 B.
B.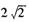 C. 4 D.
C. 4 D.