题目内容

已知点P是椭圆C：
x2
8
+
y2
4
=1上的动点，F1，F2分别为左、右焦点，O为坐标原点，则
||PF1|-|PF2||
|OP|
的取值范围是（　　）
A、[0，
2
2
]
B、[0，2）
C、(
1
2
，
2
2
]
D、[0，
2
]
分析：根据三角中线的性质可知
OP
=-
PF1
+
PF2
2
，代入
||PF1|-|PF2||
|OP|
中，根据当点P在短轴端点时||PF1|-PF2||的值最小；当点P在长轴端点时||PF1|-PF2||的值最大，进而求得答案．
解答：解：O为F1F2的中点
∴
OP
=-
PF1
+
PF2
2

∴
||PF1|-|PF2||
|OP|
=
||PF 1|-|PF 2||
|PF 1|+|PF 2|
2
=
||PF 1|-|PF 2||
2

∵当点P在短轴端点时，|PF1|=|PF2|．||PF1|-PF2||的值最小为0
当点P在长轴端点时||PF1|-PF2||的值最大为4
∴
||PF1|-|PF2||
|OP|
的取值范围是[0，
2
]
故选D
点评：本题主要考查了椭圆的应用．解题的关键是利用了三角形中线的性质．若AD是△ABC的中线，则
AB
+
AC
=2
AD
．
练习册系列答案
相关题目
已知点P是椭圆
x2
36
+
y2
24
=1(x≠0，y≠0)上的动点，F1，F2为椭圆的两个焦点，O是坐标原点，若M是∠F1PF2的角平分线上一点，且
F1M
•
MP
=0，则|OM|的取值范围是（　　）
（2013•鹰潭一模）已知点P是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）上的点，椭圆短轴长为2，F1，F2是椭圆的两个焦点，|OP|=
10
2
，
PF1
•
PF2
=
1
2
（点O为坐标原点）．
（Ⅰ）求椭圆C的方程及离心率；
（Ⅱ）直线y=x与椭圆C在第一象限交于A点，若椭圆C上两点M、N使
OM
+
ON
=λ
OA
，λ∈（0，2）求△OMN面积的最大值．
已知点P是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）上的点，椭圆短轴长为2，F1，F2是椭圆的两个焦点，|OP|=
10
2
，
PF1
•
PF2
=
1
2
（点O为坐标原点）．
（Ⅰ）求椭圆C的方程及离心率；
（Ⅱ）直线y=x与椭圆C在第一象限交于A点，若椭圆C上两点M、N使
OM
+
ON
=λ
OA
，λ∈（0，2）求△OMN面积的最大值．
已知点P是椭圆C：+=1（a＞b＞0）上的点，椭圆短轴长为2，F1，F2是椭圆的两个焦点，|OP|=，•=（点O为坐标原点）．
（Ⅰ）求椭圆C的方程及离心率；
（Ⅱ）直线y=x与椭圆C在第一象限交于A点，若椭圆C上两点M、N使+=λ，λ∈（0，2）求△OMN面积的最大值．
已知点P是椭圆：（x≠0，y≠0）上的动点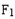，，是椭圆的两个焦点，O是坐标原点，若M是∠P的角平分线上一点，且·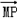=0，则|OM|的取值范围是（  ）
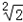A．[0，3） 
B．（0，）  
C．[，3）  
D．[0，4]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网