题目内容
已知点P是椭圆C: +
+ =1(a>b>0)上的点,椭圆短轴长为2,F1,F2是椭圆的两个焦点,|OP|=
=1(a>b>0)上的点,椭圆短轴长为2,F1,F2是椭圆的两个焦点,|OP|= ,
, •
• =
= (点O为坐标原点).
(点O为坐标原点).(Ⅰ)求椭圆C的方程及离心率;
(Ⅱ)直线y=x与椭圆C在第一象限交于A点,若椭圆C上两点M、N使
 +
+ =λ
=λ ,λ∈(0,2)求△OMN面积的最大值.
,λ∈(0,2)求△OMN面积的最大值.
【答案】分析:(Ⅰ)利用椭圆短轴长为2,求b.利用,|OP|= ,
, •
• =
= ,可求c,进而求出椭圆方程和离心率.
,可求c,进而求出椭圆方程和离心率.
(Ⅱ)将直线方程和椭圆方程联立,进行消元,转化为一元二次方程问题,然后利用根与系数之间的关系进行求解.
解答: 解:(Ⅰ)设P(x,y),F1(-c,0),F2(c,0)由|OP|=
解:(Ⅰ)设P(x,y),F1(-c,0),F2(c,0)由|OP|= ,得
,得 ,…(1分)
,…(1分)
由 •
• =
= 得
得 ,即
,即 …(2分)
…(2分)
所以c= ,又因为短轴长为2,所以b=1,所以离心率e=
,又因为短轴长为2,所以b=1,所以离心率e= ,…(4分)
,…(4分)
椭圆C的方程为: ;…(6分)
;…(6分)
(Ⅱ)解法一:由 得
得 ,设直线MN的方程为y=kx+m,
,设直线MN的方程为y=kx+m,
联立方程组 消去y得:(1+3k2)x2+6kmx+3m2-3=0…(7分)
消去y得:(1+3k2)x2+6kmx+3m2-3=0…(7分)
设M(x1,y1),N(x2,y2),则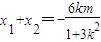 ,
, …(8分)
…(8分)
所以 .
.
因为 +
+ =λ
=λ ,λ∈(0,2),所以
,λ∈(0,2),所以 ,
, ,
,
得 ,于是
,于是 ,
, …(9分)
…(9分)
所以 …(10分)
…(10分)
又因为λ>0,原点O到直线MN的距离为 所以
所以 =
= ,
,
当 ,即
,即 时等号成立,S△OMN的最大值为
时等号成立,S△OMN的最大值为 …(13分)
…(13分)
点评:本题主要考查了椭圆的方程和性质,以及直线与椭圆的位置关系.综合性较强,运算量较大.
 ,
, •
• =
= ,可求c,进而求出椭圆方程和离心率.
,可求c,进而求出椭圆方程和离心率.(Ⅱ)将直线方程和椭圆方程联立,进行消元,转化为一元二次方程问题,然后利用根与系数之间的关系进行求解.
解答:
 解:(Ⅰ)设P(x,y),F1(-c,0),F2(c,0)由|OP|=
解:(Ⅰ)设P(x,y),F1(-c,0),F2(c,0)由|OP|= ,得
,得 ,…(1分)
,…(1分)由
 •
• =
= 得
得 ,即
,即 …(2分)
…(2分)所以c=
 ,又因为短轴长为2,所以b=1,所以离心率e=
,又因为短轴长为2,所以b=1,所以离心率e= ,…(4分)
,…(4分)椭圆C的方程为:
 ;…(6分)
;…(6分)(Ⅱ)解法一:由
 得
得 ,设直线MN的方程为y=kx+m,
,设直线MN的方程为y=kx+m,联立方程组
 消去y得:(1+3k2)x2+6kmx+3m2-3=0…(7分)
消去y得:(1+3k2)x2+6kmx+3m2-3=0…(7分)设M(x1,y1),N(x2,y2),则
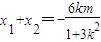 ,
, …(8分)
…(8分)所以
 .
.因为
 +
+ =λ
=λ ,λ∈(0,2),所以
,λ∈(0,2),所以 ,
, ,
,得
 ,于是
,于是 ,
, …(9分)
…(9分)所以
 …(10分)
…(10分)又因为λ>0,原点O到直线MN的距离为
 所以
所以 =
= ,
,当
 ,即
,即 时等号成立,S△OMN的最大值为
时等号成立,S△OMN的最大值为 …(13分)
…(13分)点评:本题主要考查了椭圆的方程和性质,以及直线与椭圆的位置关系.综合性较强,运算量较大.

练习册系列答案
相关题目
已知点P是椭圆C:
+
=1上的动点,F1,F2分别为左、右焦点,O为坐标原点,则
的取值范围是( )
| x2 |
| 8 |
| y2 |
| 4 |
| ||PF1|-|PF2|| |
| |OP| |
A、[0,
| ||||||
| B、[0,2) | ||||||
C、(
| ||||||
D、[0,
|
 上的动点,F1、F2分别为左、右焦点,O为坐标原点,则
上的动点,F1、F2分别为左、右焦点,O为坐标原点,则 的取值范围是
的取值范围是 上的动点,F1,F2分别为左、右焦点,O为坐标原点,则
上的动点,F1,F2分别为左、右焦点,O为坐标原点,则 的取值范围是( )
的取值范围是( )

