题目内容
已知点P是椭圆C:
+
=1(a>b>0)上的点,椭圆短轴长为2,F1,F2是椭圆的两个焦点,|OP|=
,
•
=
(点O为坐标原点).
(Ⅰ)求椭圆C的方程及离心率;
(Ⅱ)直线y=x与椭圆C在第一象限交于A点,若椭圆C上两点M、N使
+
=λ
,λ∈(0,2)求△OMN面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| PF1 |
| PF2 |
| 1 |
| 2 |
(Ⅰ)求椭圆C的方程及离心率;
(Ⅱ)直线y=x与椭圆C在第一象限交于A点,若椭圆C上两点M、N使
| OM |
| ON |
| OA |

(Ⅰ)设P(x0,y0),F1(-c,0),F2(c,0)由|OP|=
| ||
| 2 |
| 5 |
| 2 |
由
| PF1 |
| PF2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以c=
| 2 |
| c |
| a |
| ||
| 3 |
椭圆C的方程为:
| x2 |
| 3 |
(Ⅱ)解法一:由
|
| ||
| 2 |
| ||
| 2 |
联立方程组
|
设M(x1,y1),N(x2,y2),则x1+x2=-
| 6km |
| 1+3k2 |
| 3m2-3 |
| 1+3k2 |
所以y1+y2=k(x1+x2)+2m=
| 2m |
| 1+3k2 |
因为
| OM |
| ON |
| OA |
| ||
| 2 |
| ||
| 2 |
得kMN=-
| 1 |
| 3 |
| ||
| 3 |
| 3m |
| 2 |
| 9m2-9 |
| 4 |
所以|MN|=
1+(-
|
| ||
| 3 |
| (x1+x2)2-4x1x2 |
| ||||
| 2 |
又因为λ>0,原点O到直线MN的距离为d=
3
| ||
| 10 |
| 1 |
| 2 |
| ||||
| 4 |
3
| ||
| 10 |
| 1 |
| 2 |
| ||||
| 4 |
3
| ||
| 10 |
| ||||
| 4 |
| ||
| 2 |
当m=
| ||
| 3 |
| 2 |
| ||
| 2 |

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 +
+ =1(a>b>0)上的点,椭圆短轴长为2,F1,F2是椭圆的两个焦点,|OP|=
=1(a>b>0)上的点,椭圆短轴长为2,F1,F2是椭圆的两个焦点,|OP|= ,
, •
• =
= (点O为坐标原点).
(点O为坐标原点). +
+ =λ
=λ ,λ∈(0,2)求△OMN面积的最大值.
,λ∈(0,2)求△OMN面积的最大值. (x≠0,y≠0)上的动点,
(x≠0,y≠0)上的动点,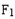 ,
, 是椭圆的两个焦点,O是坐标原点,若M是∠
是椭圆的两个焦点,O是坐标原点,若M是∠ P
P 的角平分线上一点,且
的角平分线上一点,且 ·
·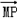 =0,则|OM|的取值范围是( )
=0,则|OM|的取值范围是( )  )
) 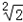 ,3)
,3)