题目内容
如图,在直角梯形ABCD中,∠B=∠C=90°,AB=| 2 |
| ||
| 2 |
(1)求该几何体的体积V;
(2)设直角梯形ABCD绕底边AB所在的直线旋转角θ(∠CBC′=θ∈(0,π))至ABC′D′,问:是否存在θ,使得AD′⊥DC′.若存在,求角θ的值,若不存在,请说明理由.
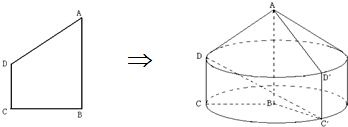
分析:(1)在直角梯形ABCD作DE⊥AB,则作DE是圆锥的底面半径,AE是它的高,而BC和CD是圆柱的半径和母线,根据题意分别求出并代入椎体和柱体的体积公式,进行求和求出旋转体得体积;
(2)先假设存在θ满足题意,再根据AD′⊥DC′和余弦定理进行求解,求出对应一个角的余弦值大于0,与线线垂直矛盾,故证出假设不成立即不存在.
(2)先假设存在θ满足题意,再根据AD′⊥DC′和余弦定理进行求解,求出对应一个角的余弦值大于0,与线线垂直矛盾,故证出假设不成立即不存在.
解答: 解:(1)如图,
解:(1)如图,
作DE⊥AB,则由已知,得DE=1,AE=AB-EB=
,
∴V=
π×12×
+π×12×
=
π.
(2)取BA的中点E,连DE,C′E,则∠DC′E(或其补角)就是异面直线AD′与DC′所成的角.
在△DC′E中,EC′=AD′=
,DE=CB=1,CC'2=1+1-2cosθ=2-2cosθDC′2=DC2+CC′2=
+(1+1-2cosθ)=
-2cosθ,
∴cos∠DC′E=
=
>0,
故不存在θ,使得AD′⊥DC′.
 解:(1)如图,
解:(1)如图,作DE⊥AB,则由已知,得DE=1,AE=AB-EB=
| ||
| 2 |
∴V=
| 1 |
| 3 |
| ||
| 2 |
| ||
| 2 |
2
| ||
| 3 |
(2)取BA的中点E,连DE,C′E,则∠DC′E(或其补角)就是异面直线AD′与DC′所成的角.
在△DC′E中,EC′=AD′=
| ||
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴cos∠DC′E=
| DC′2+EC′2-DE2 |
| 2EC′•C′D |
| 3-2cosθ |
| 2EC′•C′D |
故不存在θ,使得AD′⊥DC′.
点评:本题是有关旋转体的综合题,需要根据题意求出几何体的几何元素的长度,再求出它的体积;对存在性问题的处理办法,一般是先假设存在再根据题意列出关系,证明结果是否有矛盾即可,考查了分析和解决问题的能力.

练习册系列答案
相关题目
 如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=
如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD= 如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD,
如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD, 如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设
如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设 如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则
如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则