题目内容
已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( ).
| A.-1<a<2 | B.-3<a<6 |
| C.a<-1或a>2 | D.a<-3或a>6 |
D
解析试题分析:因为f(x)=x3+ax2+(a+6)x+1有极大值和极小值,所以,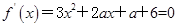 有不等实根,
有不等实根,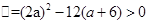 ,解得,a<-3或a>6,故选D。
,解得,a<-3或a>6,故选D。
考点:本题主要考查利用导数研究函数的极值。
点评:简单题,连续函数存在极值,函数的导数为零必有解。

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
已知 ,且
,且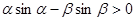 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
A.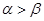 | B.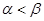 |
C.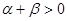 | D.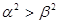 |
函数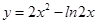 的的单调递增区间是 ( )
的的单调递增区间是 ( )
A.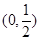 | B.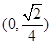 |
C.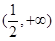 | D.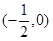 和 和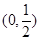 |
求曲线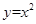 与
与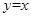 所围成图象的面积,其中正确的是( )
所围成图象的面积,其中正确的是( )
A.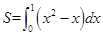 | B.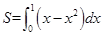 |
C.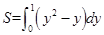 | D.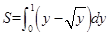 |
如图,由函数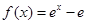 的图象,直线
的图象,直线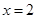 及x轴所围成的阴影部分面积等于( )
及x轴所围成的阴影部分面积等于( )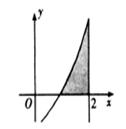
A.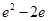 | B.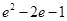 |
C.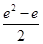 | D.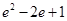 |
如图,是函数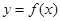 的导函数
的导函数 的图象,则下面判断正确的是
的图象,则下面判断正确的是
A.在区间(-2,1)上 是增函数; 是增函数; |
B.在区间(1,2)上 是减函数; 是减函数; |
C. 有一个极大值,两个极小值; 有一个极大值,两个极小值; |
D.当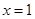 时, 时, 取极大值, 取极大值,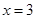 , , 取极小值. 取极小值. |
设函数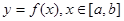 ,其导函数的图象如图所示,则函数
,其导函数的图象如图所示,则函数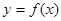 的减区间是
的减区间是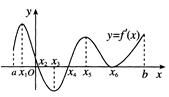
A.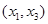 | B.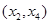 |
C.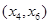 | D.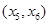 |
已知积分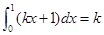 ,则实数
,则实数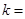 ( )
( )
| A.2 | B.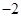 | C.1 | D.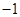 |
已知函数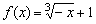 ,则
,则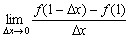 的值为( )
的值为( )
A.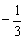 | B.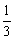 | C.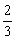 | D.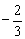 |