题目内容
(本小题14分)
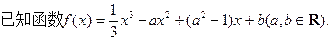
(Ⅰ)若
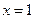 为
为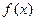 的极值点,求
的极值点,求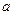 的值;
的值;(Ⅱ)若
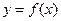 的图象在点
的图象在点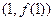 处的切线方程为
处的切线方程为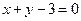 ,求
,求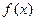 在区间
在区间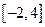 上的最大值;
上的最大值;(Ⅲ)当
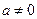 时,若
时,若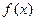 在区间
在区间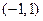 上不单调,求
上不单调,求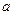 的取值范围.
的取值范围.解:(Ⅰ)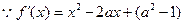 …………………………………………………1分
…………………………………………………1分
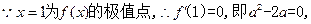 ………………………………………2分
………………………………………2分
∴a=0或2. …………………………………………………………………………………4分
(Ⅱ)∵(1,f(1))是 切点,
切点,
∴1+f(1)-3=0, ∴f(1)=2……………………………………………………………………5分
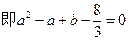
∵切线方程x+y-3=0的斜率为-1,
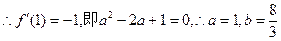 ………………………………………………7分
………………………………………………7分
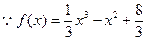
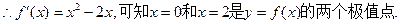 …………………………8分
…………………………8分
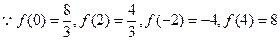 ………………………………………………9分
………………………………………………9分
∴y=f(x)在区间[-2,4]上的最大值为8. ……………………………………………………10分
(Ⅲ)因为函数f(x)在区间(-1,1)不单调,所以函数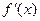 在(-1,1)上存在零点.
在(-1,1)上存在零点.
而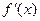 =0的两根为a-1,a+1,区间长为2,
=0的两根为a-1,a+1,区间长为2,
∴在区间(-1,1)上不可能有2个零点. …………………………………………………11分
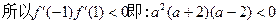 ……………………………………………12分
……………………………………………12分
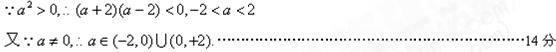
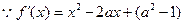 …………………………………………………1分
…………………………………………………1分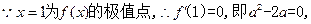 ………………………………………2分
………………………………………2分∴a=0或2. …………………………………………………………………………………4分
(Ⅱ)∵(1,f(1))是
 切点,
切点,∴1+f(1)-3=0, ∴f(1)=2……………………………………………………………………5分
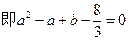
∵切线方程x+y-3=0的斜率为-1,
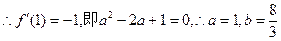 ………………………………………………7分
………………………………………………7分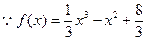
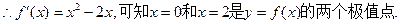 …………………………8分
…………………………8分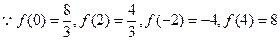 ………………………………………………9分
………………………………………………9分∴y=f(x)在区间[-2,4]上的最大值为8. ……………………………………………………10分
(Ⅲ)因为函数f(x)在区间(-1,1)不单调,所以函数
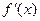 在(-1,1)上存在零点.
在(-1,1)上存在零点.而
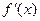 =0的两根为a-1,a+1,区间长为2,
=0的两根为a-1,a+1,区间长为2,∴在区间(-1,1)上不可能有2个零点. …………………………………………………11分
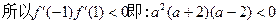 ……………………………………………12分
……………………………………………12分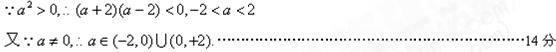
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

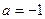 时,求函数的单调区间。
时,求函数的单调区间。 时,讨论函数的单调增区间。
时,讨论函数的单调增区间。 ,使
,使 ,函数有最小值-3?
,函数有最小值-3?
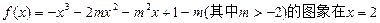 处的切线与直线
处的切线与直线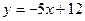 平行.
平行. 的值;
的值; 在区间[0,1]的最小值;
在区间[0,1]的最小值; ,根据上述(I)
,根据上述(I) 、(II)的结论,证明:
、(II)的结论,证明:
 +
+ +
+ =
= ,
, +
+ +
+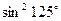 =
=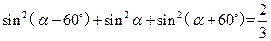
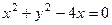 在点
在点 处的切线方程为( )
处的切线方程为( )

 B
B
 D
D
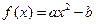 在区间
在区间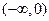 内是减函数,则
内是减函数,则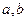 应满足( )
应满足( ) 且
且
 且
且

 ,若
,若 ,则
,则 的值等于( )
的值等于( )
 B
B C
C D
D
 lnx的导数是_____
lnx的导数是_____