题目内容
12.如图(1),在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2.将△ADC沿AC折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图所示(2).
(1)求几何体D-ABC的体积;
(2)求二面角D-AB-C的正切值;
(3)求几何体D-ABC的外接球的表面积.
分析 (1)由高和底面积,求得三棱锥B-ACD的体积即是几何体D-ABC的体积.
(2)记AC中点为E,过E作EH⊥AB,连结DE,DH,证明∠DHE是二面角D-AB-C的平面角,即可求二面角D-AB-C的正切值;
(3)O为AB中点,E为AC中点,连结DE,EO,DO,D-ABC的外接球的球心为O,半径为2,即可求几何体D-ABC的外接球的表面积.
解答  解:(1)在直角梯形中,知AC=BC=2$\sqrt{2}$,∴AC2+BC2=AB2,∴AC⊥BC
解:(1)在直角梯形中,知AC=BC=2$\sqrt{2}$,∴AC2+BC2=AB2,∴AC⊥BC
取AC中点O,连接DO,则DO⊥AC,又平面ADC⊥平面ABC,
且平面ADC∩平面ABC=AC,DO?平面ACD,从而OD⊥平面ABC,
∴OD⊥BC,
又AC⊥BC,AC∩OD=O,
∴BC⊥平面ACD,
∵S△ACD=$\frac{1}{2}$×2×2=2,
∴三棱锥B-ACD的体积为:$\frac{1}{3}×2×2\sqrt{2}$=$\frac{4\sqrt{2}}{3}$,
由等积性知几何体D-ABC的体积为:$\frac{4\sqrt{2}}{3}$;
(2)记AC中点为E,过E作EH⊥AB,连结DE,DH,
∵AD=DC,E为AC中点,
∴DE⊥AC,
∵平面平面ACD⊥平面ABC,平面ACD∩平面ABC=AC,
∴DE⊥平面ACB,
∴DE⊥AB,
又∵EH⊥AB,且DE∩HE=E,
∴AB⊥平面DHE,
∴DH⊥AB,
∴∠DHE是二面角D-AB-C的平面角.
∵DE=$\sqrt{2}$,HE=1,
∴tan∠DHE=$\sqrt{2}$;
(3)O为AB中点,E为AC中点,连结DE,EO,DO,
∵DE⊥平面ACB,DE=OE=$\sqrt{2}$,
∴DE⊥OE,DO=2.
又∵AO=BO=CO=2,
∴D-ABC的外接球的球心为O,半径为2,
∴D-ABC的外接球的表面积为16π.
点评 本题通过平面图形折叠后得立体图形,考查空间中的垂直关系,重点是“线线垂直,线面垂直,面面垂直”的转化;等积法求体积,也是常用的数学方法.

| 年份(x) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数(y) | 3 | 5 | 8 | 11 | 13 | 14 | 17 | 22 | 30 | 31 |
(Ⅱ)根据前5年的数据,利用最小二乘法求出y关于x的回归方程y=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并计算2013年的估计值和实际值之间的差的绝对值.
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| A. | [1,2] | B. | (1,2] | C. | (1,+∞) | D. | [-2,2] |
| A. | 32(5) | B. | 23(5) | C. | 21(5) | D. | 12(5) |
| A. | 9801 | B. | 9950 | C. | 10000 | D. | 10201 |
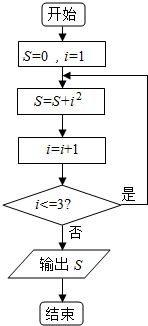 阅读如图的程序框图,则输出的S=( )
阅读如图的程序框图,则输出的S=( )| A. | 14 | B. | 20 | C. | 30 | D. | 55 |
 如图,已知圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.
如图,已知圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2. 从参加环保知识竞赛的学生中抽出60名,将其成绩整理后画出的频率分布直方图如图.观察图形,回答下列问题:
从参加环保知识竞赛的学生中抽出60名,将其成绩整理后画出的频率分布直方图如图.观察图形,回答下列问题: