题目内容
4.(1)求函数y=$\sqrt{{x}^{2}+x+1}$的值域.(2)画出y=2|x-1|的图象.
分析 (1)先求出定义域,求出x2+x+1在定义域上的范围,再求出函数的值域;
(2)将函数y=2x向右平移1个单位得到y=2x-1的图象,在作出关于直线x=1对称的图象即可,注意自变量的取值范围.
解答 解:(1)由式子有意义得x2+x+1≥0,
解得x∈R.
令t=x2+x+1=(x+$\frac{1}{2}$)2+$\frac{3}{4}$≥$\frac{3}{4}$,
∴y=$\sqrt{{x}^{2}+x+1}$=$\sqrt{t}$≥$\frac{\sqrt{3}}{2}$,
∴函数y=$\sqrt{{x}^{2}+x+1}$的值域是[$\frac{\sqrt{3}}{2}$,+∞).
(2)作出函数图象如图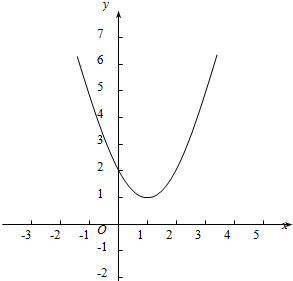
点评 本题考查了函数的单调性,函数图象变换,是基础题.

练习册系列答案
相关题目
15.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{2}x|(0<x≤2)}\\{-\frac{1}{2}x+2(x>2)}\end{array}\right.$,若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是( )
| A. | (1,4) | B. | (2,4) | C. | (0,8) | D. | (2,8) |
9.已知双曲线${x^2}-\frac{y^2}{8}=1$的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则$\overrightarrow{P{A_1}}•\overrightarrow{P{F_2}}$的最小值为( )
| A. | -4 | B. | $-\frac{81}{16}$ | C. | 1 | D. | 0 |
14.某厂生产甲、乙两种产品每吨所需的煤、电和产值如表所示.
但国家每天分配给该厂的煤、电有限,每天供煤至多47吨,供电至多300千瓦,问该厂如何安排生产,使得该厂日产值最大?最大日产值为多少?
| 用煤(吨) | 用电(千瓦) | 产值(万元) | |
| 甲产品 | 3 | 50 | 12 |
| 乙产品 | 7 | 20 | 8 |
