题目内容
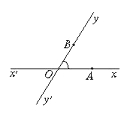
【题目】如图，有两条相交成60°角的直线xx′，yy′，交点是O，甲、乙分别在Ox，Oy上，起初甲离O点3 km，乙离O点1 km，后来两人同时用每小时4 km的速度，甲沿xx′方向，乙沿y′y方向步行，问：
（1）用包含t的式子表示t小时后两人的距离；
（2）什么时候两人的距离最短？
【答案】（1）
（2）在第15分钟末，PQ最短，最短距离为2 km
【解析】
试题分析：（1）设两人的距离为ykm根据题意分两种情况讨论即A与O不重合，A和O重合，分别利用三角函数求出AB即可得到y的解析式；（2）利用二次函数求最小值的方法求出y的最小值即可
试题解析：（1）设甲、乙两人t小时后的位置分别是P、Q，
则AP＝4t，BQ＝4t
(Ⅰ)当0≤t≤
时，
PQ＝
＝
(Ⅱ)当t＞
时，
PQ＝
＝
综上（Ⅰ）、（Ⅱ）可知PQ＝＝
（2）∵PQ2＝48(t－
)2＋4 ∴当t＝
时，（PQ）min＝2
即在第15分钟末，PQ最短，最短距离为2 km.
练习册系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
