��Ŀ����
�������⣺
��1��������f��x��=lg��x+
����Ϊ�溯������a=1��
��2������f��x��=|sinx|������T=��
��3����֪
=(sin�ȣ�
)��
=(1��
)�����Цȡʣ��У�
������
��
��4���ڡ�ABC�У�
=a��
=b����a•b��0�����ABC�Ƕ۽�������
�� 5��O�ǡ�ABC����ƽ����һ���㣬����P���㣺
=
+��(
+
)���ˡʣ�0��+�ޣ�����ֱ��APһ��ͨ����ABC�����ģ�
�����������������
��1��������f��x��=lg��x+
| x2+a |
��2������f��x��=|sinx|������T=��
��3����֪
| a |
| 1+cos�� |
| b |
| 1-cos�� |
| 3�� |
| 2 |
| a |
| b |
��4���ڡ�ABC�У�
| BA |
| AC |
�� 5��O�ǡ�ABC����ƽ����һ���㣬����P���㣺
| OP |
| OA |
| ||
| sinC |
| ||
| sinB |
�����������������
��1����2����3����5��
��1����2����3����5��
����������1��������f��x��=lg��x+
��Ϊ�溯������f��0��=0����������a��ֵ��
��2�������Һ�����ͼ��֪���������f��x�������ڣ�
��3��д������������������������ͬ�����Ǻ����Ļ�����ϵʽ�������ɵõ����ۣ�
��4���ڡ�ABC�У�
=
��
=
��
•
��0�����BAC����ǣ��ɴ����жϡ�ABCһ���Ƕ۽������Σ�
��5���Ѹ�����ʽ�еĽǵ�����ֵ�ö�Ӧ�߳������Բ�뾶��ʾ�������������
=2R�ˣ�
+
�����ɴ�ʽ��ֱ֪��APһ��ͨ����ABC�����ģ�
| x2+a |
��2�������Һ�����ͼ��֪���������f��x�������ڣ�
��3��д������������������������ͬ�����Ǻ����Ļ�����ϵʽ�������ɵõ����ۣ�
��4���ڡ�ABC�У�
| BA |
| a |
| AC |
| b |
| a |
| b |
��5���Ѹ�����ʽ�еĽǵ�����ֵ�ö�Ӧ�߳������Բ�뾶��ʾ�������������
| AP |
| ||
|
|
| ||
|
|
����⣺������f��x��=lg��x+
��Ϊ�溯����
��f��0��=lg��0+
��=lg
=0�����a=1���ʣ�1��������
�����Һ�����ͼ��֪����f��x��=|sinx|������T=�У��ʣ�2��������
��
=(sin�ȣ�
)��
=(1��
)�����Цȡʣ��У�
����
��
•
=sin��+
=sin��-sin��=0��
��
��
���ʣ�3��������
�ڡ�ABC�У�
=
��
=
��
•
��0��
���BAC����ǣ���ABC��һ���Ƕ۽������Σ��ʣ�4����������
��ͼ��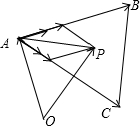
�ڡ�ABC�У���
=
=2R��RΪ������ABC���Բ�뾶����
����sinC=
��sinB=
��
����
=
+�ˣ�
+
��=
+�ˣ�
+
��=
+2R�ˣ�
+
����
��
=2R�ˣ�
+
����
����ֱ��APһ��ͨ����ABC�����ģ��ʣ�5����ȷ��
�ʴ�Ϊ����1����2����3����5����
| x2+a |
��f��0��=lg��0+
| 0+a |
| a |
�����Һ�����ͼ��֪����f��x��=|sinx|������T=�У��ʣ�2��������
��
| a |
| 1+cos�� |
| b |
| 1-cos�� |
| 3�� |
| 2 |
��
| a |
| b |
| 1-cos2�� |
��
| a |
| b |
�ڡ�ABC�У�
| BA |
| a |
| AC |
| b |
| a |
| b |
���BAC����ǣ���ABC��һ���Ƕ۽������Σ��ʣ�4����������
��ͼ��

�ڡ�ABC�У���
|
| ||
| sinC |
|
| ||
| sinB |
����sinC=
|
| ||
| 2R |
|
| ||
| 2R |
����
| OP |
| OA |
| ||
| sinC |
| ||
| sinB |
| OA |
2R
| ||
|
|
2R
| ||
|
|
| OA |
| ||
|
|
| ||
|
|
��
| AP |
| ||
|
|
| ||
|
|
����ֱ��APһ��ͨ����ABC�����ģ��ʣ�5����ȷ��
�ʴ�Ϊ����1����2����3����5����
���������⿼�����������ٵ��ж������ã����е��⣮����ʱҪ�������⣬ע���溯���������������������Ǻ��������Ҷ�����֪ʶ��ĺ������ã�

��ϰ��ϵ�д�
 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д� ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д�
�����Ŀ
 ��0��x��1���������ֵΪ
��0��x��1���������ֵΪ ��
�� ��
�� ��
��