题目内容
知{an}是首项为-2的等比数列,Sn是其前n项和,且S3,S2,S4成等差数列,
(1)求数列{an}的通项公式.
(2)若bn=log2|an|,求数列{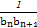 }的前n项和Tn.
}的前n项和Tn.
(1)求数列{an}的通项公式.
(2)若bn=log2|an|,求数列{
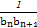 }的前n项和Tn.
}的前n项和Tn.(1) an=(-2)n (2) Tn=1-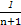 =
=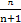
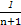 =
=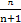
(1)设数列{an}的公比为q,其首项a1=-2.
方法一:①若q=1,则Sn=na1=-2n,
此时S3=-6,S2=-4,S4=-8,S3,S2,S4不成等差数列,不合题意;
②若q≠1,则Sn=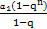 =-
=-
因为S3,S2,S4成等差数列,
所以2S2=S3+S4,即-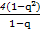 =-
=-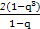 -
- ,
,
整理得q2+q-2=0,
解得q=-2或q=1(舍去),
综上所述,数列{an}的通项公式为an=a1qn-1
=(-2)×(-2)n-1=(-2)n.
方法二:S2=a1+a1q,S3=a1+a1q+a1q2,S4=a1+a1q+a1q2+a1q3.
因为S3,S2,S4成等差数列,
所以2S2=S3+S4,即2a1+2a1q=2a1+2a1q+2a1q2+a1q3,整理得2a1q2+a1q3=0.
因为a1≠0,q≠0,所以q=-2,
故数列{an}的通项公式为an=a1qn-1=(-2)×(-2)n-1=(-2)n.
(2)由(1)可知an=(-2)n,
依题意bn=log2|an|=log2|(-2)n|=log22n=n,
所以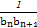 =
= =
= -
-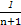 ,
,
所以Tn=(1- )+(
)+( -
- )+…+(
)+…+( -
-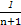 )=1-
)=1-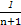 =
=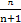 .
.
方法一:①若q=1,则Sn=na1=-2n,
此时S3=-6,S2=-4,S4=-8,S3,S2,S4不成等差数列,不合题意;
②若q≠1,则Sn=
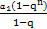 =-
=-
因为S3,S2,S4成等差数列,
所以2S2=S3+S4,即-
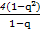 =-
=-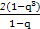 -
- ,
,整理得q2+q-2=0,
解得q=-2或q=1(舍去),
综上所述,数列{an}的通项公式为an=a1qn-1
=(-2)×(-2)n-1=(-2)n.
方法二:S2=a1+a1q,S3=a1+a1q+a1q2,S4=a1+a1q+a1q2+a1q3.
因为S3,S2,S4成等差数列,
所以2S2=S3+S4,即2a1+2a1q=2a1+2a1q+2a1q2+a1q3,整理得2a1q2+a1q3=0.
因为a1≠0,q≠0,所以q=-2,
故数列{an}的通项公式为an=a1qn-1=(-2)×(-2)n-1=(-2)n.
(2)由(1)可知an=(-2)n,
依题意bn=log2|an|=log2|(-2)n|=log22n=n,
所以
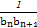 =
= =
= -
-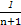 ,
,所以Tn=(1-
 )+(
)+( -
- )+…+(
)+…+( -
-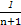 )=1-
)=1-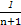 =
=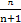 .
.
练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
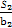 .
. ≤
≤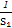 +
+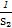 +…+
+…+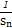 <
< .
.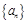 的前
的前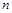 项和为
项和为 ,并满足:
,并满足: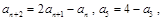 则
则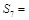 ( )
( ) <-1,且它的前n项和Sn有最大值,则使得Sn<0的n的最小值为( )
<-1,且它的前n项和Sn有最大值,则使得Sn<0的n的最小值为( ) ,则S10等于( )
,则S10等于( )


