题目内容
【题目】已知集合M是满足下列性质的函数![]() 的全体:在定义域内存在
的全体:在定义域内存在![]() 使得
使得![]() 成立。
成立。
(1)函数![]() 是否属于集合M?请说明理由;
是否属于集合M?请说明理由;
(2)函数![]() M,求a的取值范围;
M,求a的取值范围;
(3)设函数![]() ,证明:函数
,证明:函数![]() M。
M。
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)直接进行验证或用反证法求解;(2)由![]() M得到方程
M得到方程![]() 在定义域内有解,然后转化成二次方程的问题求解;(3)验证函数
在定义域内有解,然后转化成二次方程的问题求解;(3)验证函数![]() 满足
满足![]() 即可得到结论成立.
即可得到结论成立.
(1)![]() .理由如下:
.理由如下:
假设![]() ,
,
则在定义域内存在![]() ,使得
,使得![]() 成立,
成立,
即![]() ,
,
整理得![]() ,
,
∵方程![]() 无实数解,
无实数解,
∴假设不成立,
∴![]() .
.
(2)由题意得![]() ,
,
![]() 在定义域内有解,
在定义域内有解,
即![]() 在实数集R内有解,
在实数集R内有解,
当![]() 时,
时,![]() ,满足题意;
,满足题意;
当![]() 时,由
时,由![]() ,得
,得![]() ,
,
解得![]() 且
且![]() ,
,
综上![]() ,
,
∴实数a的取值范围为![]() .
.
(3)证明:∵![]() ,
,
∴![]() ,
,
又函数![]() 的图象与函数
的图象与函数![]() 的图象有交点,
的图象有交点,
设交点的横坐标为a,则![]() ,
,
∴![]() ,其中
,其中![]() ,
,
∴ 存在![]() 使得
使得![]() 成立,
成立,
∴![]() .
.

【题目】(2017全国Ⅱ,文19)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:

旧养殖法
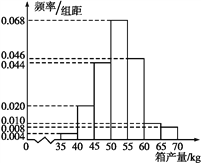
新养殖法
(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关;
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:![]() ,
,
【题目】已知某海滨浴场海浪的高度y(米)是时间t(0≤t≤24,单位:时)的函数,记作:![]() .下表是某日各时的浪高数据.
.下表是某日各时的浪高数据.
t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
(1)根据以上数据,求函数y=f(t)的函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00时至晚上20:00时之间,有多少时间可供冲浪者进行运动?
