题目内容
已知两个平面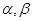 ,直线
,直线 ,则“
,则“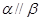 ”是“直线
”是“直线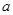
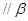 ”的 ( )
”的 ( )
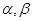 ,直线
,直线 ,则“
,则“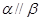 ”是“直线
”是“直线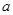
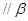 ”的 ( )
”的 ( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
分析:根据面面平行的定义可知“α∥β”?“直线a∥β”是真命题,而“直线a∥β”?“α∥β”是假命题,根据若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件进行判断即可.
解答:解:根据面面平行的定义可知α与β无公共点,而a?α,则a与β无公共点,则直线a∥β
即“α∥β”?“直线a∥β”是真命题;
直线a?α,直线a∥β?两个平面α、β可能平行也可能相交,
即“直线a∥β”?“α∥β”是假命题;
根据充要条件的判定可知“α∥β”是“直线a∥β”的充分不必要条件
故选A
解答:解:根据面面平行的定义可知α与β无公共点,而a?α,则a与β无公共点,则直线a∥β
即“α∥β”?“直线a∥β”是真命题;
直线a?α,直线a∥β?两个平面α、β可能平行也可能相交,
即“直线a∥β”?“α∥β”是假命题;
根据充要条件的判定可知“α∥β”是“直线a∥β”的充分不必要条件
故选A

练习册系列答案
相关题目
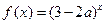 是增函数,若p或q为真,p且q为假,求实数a的取值范围.
是增函数,若p或q为真,p且q为假,求实数a的取值范围.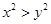 ,则
,则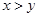 ”的逆否命题是( )
”的逆否命题是( )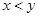 ,则
,则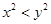 ”
”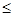
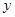 ,则
,则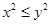 ”
”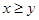 ,则
,则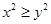 ”
”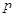 :存在
:存在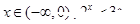 ;命题
;命题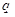 :
: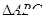 中,若
中,若 ,则
,则 ,则下列命题中为真命题的是( )
,则下列命题中为真命题的是( )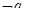 )
)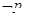 )且
)且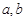 为两条不同的直线,
为两条不同的直线,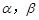 为两个不同的平面,则下列命题正确的是( )
为两个不同的平面,则下列命题正确的是( )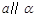 ,
,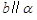 ,则
,则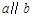
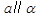 ,
,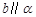
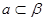 ,
,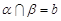 ,则
,则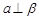 ,
,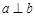 ,则
,则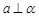
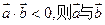 的夹角为钝角; 高#考#资#源#
的夹角为钝角; 高#考#资#源#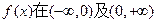 上都是增函数,则
上都是增函数,则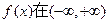

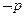 为假命题
为假命题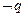 为假命题
为假命题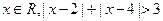 ”的否定是____▲____
”的否定是____▲____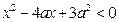 的解集为
的解集为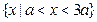 ;②若函数
;②若函数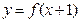 为偶函数,则
为偶函数,则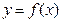 的图象关于
的图象关于 对称;③若不等式
对称;③若不等式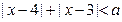 的解集为空集,必有
的解集为空集,必有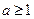 ;④函数
;④函数 至多有一个交点。其中所有正确命题的序号是______________
至多有一个交点。其中所有正确命题的序号是______________