题目内容
已知α,β均为锐角,且sinα=
,tan(α-β)=-
.
(1)求sin(α-β)的值;
(2)求cosβ的值.
| 3 |
| 5 |
| 1 |
| 3 |
(1)求sin(α-β)的值;
(2)求cosβ的值.
分析:(1)根据α、β的范围,利用同角三角函数的基本关系,求得sin(α-β)的值.
(2)由(1)可得,cos(α-β)=
,cosα=
,根据cosβ=cos[α-(α-β)],利用两角差的余弦公式求得结果.
(2)由(1)可得,cos(α-β)=
3
| ||
| 10 |
| 4 |
| 5 |
解答:解:(1)∵α,β∈(0,
),从而-
<α-β<
.
又∵tan(α-β)=-
<0,∴-
<α-β<0. …(4分)
利用同角三角函数的基本关系可得sin2(α-β)+cos2(α-β)=1,且
=-
,
解得 sin(α-β)=-
. …(6分)
(2)由(1)可得,cos(α-β)=
.∵α为锐角,sinα=
,∴cosα=
. …(10分)
∴cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β)…(12分)
=
×
+
×(-
)=
. …(14分)
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
又∵tan(α-β)=-
| 1 |
| 3 |
| π |
| 2 |
利用同角三角函数的基本关系可得sin2(α-β)+cos2(α-β)=1,且
| sin(α-β) |
| cos(α-β) |
| 1 |
| 3 |
解得 sin(α-β)=-
| ||
| 10 |
(2)由(1)可得,cos(α-β)=
3
| ||
| 10 |
| 3 |
| 5 |
| 4 |
| 5 |
∴cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β)…(12分)
=
| 4 |
| 5 |
3
| ||
| 10 |
| 3 |
| 5 |
| ||
| 10 |
9
| ||
| 50 |
点评:本题主要考查同角三角函数的基本关系,两角和差的余弦公式的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
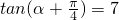 ,
, ,α,β均为锐角.
,α,β均为锐角.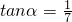 ,
,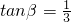 ,α,β均为锐角
,α,β均为锐角 如图,点B在以PA为直径的圆周上,点C在线段AB上,已知
如图,点B在以PA为直径的圆周上,点C在线段AB上,已知 如图,点B在以PA为直径的圆周上,点C在线段AB上,已知
如图,点B在以PA为直径的圆周上,点C在线段AB上,已知 ,设
,设 ,
, 均为锐角.
均为锐角. ;
; 的数量积
的数量积 的值.
的值.