Question

17．已知函数f（x）=$\left\{\begin{array}{l}{-1，x＜0}\\{0，x=0}\\{1，x＞0}\end{array}\right.$，试作出该函数的图象，并求f（1），f（-1），f（5），f（x²+1）和f（$\frac{1}{2}$x）的值．

Answer 1

分析 画出函数的图象，然后求出函数值即可．

解答 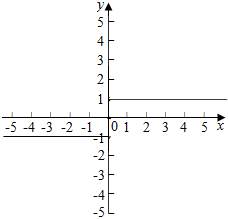解：函数f（x）=$\left\{\begin{array}{l}{-1，x＜0}\\{0，x=0}\\{1，x＞0}\end{array}\right.$，作出该函数的图象如图：
f（1）=1，
f（-1）=-1，
f（5）=1，
f（x²+1）=1，
f（$\frac{1}{2}$x）=$\left\{\begin{array}{l}-1，x＜0\\ 0，x=0\\ 1，x＞0\end{array}\right.$．

点评 本题考查函数的图象的作法，函数值的求法，考查计算能力，作图能力．