题目内容
(1)已知角α终边上一点P(-4,3),求cos(
| ||||
cos(
|
(2)求函数y=
| -sinx |
| tanx-1 |
分析:(1)由于tanα=
=
=-
,利用诱导公式可得
=
=tanα,从而求得结果.
(2)由题意得
,即
,解得 2kπ+
≤x<2kπ+
,k∈z.
| y |
| x |
| 3 |
| -4 |
| 3 |
| 4 |
cos(
| ||||
cos(
|
| -sinαsinα |
| -sinαcosα |
(2)由题意得
|
|
| 5π |
| 4 |
| 3π |
| 2 |
解答:解:(1)∵tanα=
=
=-
,
=
=tanα=-
.
(2)由题意得
,
,
2kπ+
≤x<2kπ+
,k∈z,故函数y=
+
的定义域为 {x|2kπ+
≤x<2kπ+
,k∈z}.
| y |
| x |
| 3 |
| -4 |
| 3 |
| 4 |
cos(
| ||||
cos(
|
| -sinαsinα |
| -sinαcosα |
| 3 |
| 4 |
(2)由题意得
|
|
2kπ+
| 5π |
| 4 |
| 3π |
| 2 |
| -sinx |
| tanx-1 |
| 5π |
| 4 |
| 3π |
| 2 |
点评:本题考查任意角的三角函数的定义,及诱导公式,正弦函数、正切函数的定义域和值域,得到
,
,是解题的关键.
,
|

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
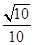 x,求sin θ,tan θ.
x,求sin θ,tan θ. ,求
,求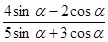 的值.
的值. ,-
,- ),求sinα、cosα、tanα的值;
),求sinα、cosα、tanα的值;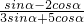 =-5,求tanα的值.
=-5,求tanα的值. ,-
,-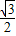 ),求sinα、cosα、tanα的值;
),求sinα、cosα、tanα的值; =-5,求tanα的值.
=-5,求tanα的值.