题目内容
（1）已知角α的终边上有一点P（
，-
），求sinα、cosα、tanα的值；
（2）已知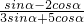
=-5，求tanα的值．
解：（1）∵角α的终边上有一点P（，-），∴x=，y=-，r=
=1，
∴sinα=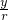
=-，cosα=
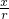=，tanα=
=-
．
（2）∵已知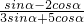=-5，∴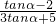
=-5，解得 tanα=-
．
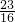分析：（1）由角α的终边上有一点P（，-），可得 x=，y=-，r==1，再由任意角的三角函数的定义求得sinα、cosα、tanα的值．
（2）由条件利用同角三角函数的基本关系可得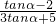=-5，解方程求得 tanα 的值．
点评：本题主要考查任意角的三角函数的定义，同角三角函数的基本关系，属于基础题．
，-），∴x=，y=-，r==1，∴sinα=
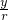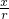=-，cosα==，tanα==-．（2）∵已知
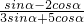=-5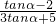，∴=-5，解得 tanα=-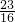．分析：（1）由角α的终边上有一点P（
，-），可得 x=，y=-，r==1，再由任意角的三角函数的定义求得sinα、cosα、tanα的值．（2）由条件利用同角三角函数的基本关系可得
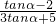=-5，解方程求得 tanα 的值．点评：本题主要考查任意角的三角函数的定义，同角三角函数的基本关系，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知角a的终边过点P（-1，2），cosa的值为（ ）
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|