题目内容
本小题满分12分)设函数f(x)= 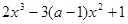 ,其中
,其中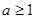
(1)求f(x)的单调区间;(2)讨论f(x)的极值
(Ⅰ)当 时,
时,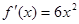 ,
, 在
在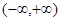 上单调递增;
上单调递增;
当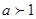 时,
时, 在
在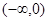 上单调递增;在
上单调递增;在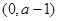 上单调递减;在
上单调递减;在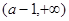 上单调递增;
上单调递增;
(Ⅱ)当 时,函数
时,函数 没有极值;
没有极值;
当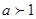 时,函数
时,函数 在
在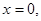 处取得极大值,在
处取得极大值,在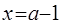 处取得极小值
处取得极小值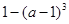 .
.
解析试题分析: (1)先求解函数的导数,然后根据导数的正负解集,需要对参数a分类讨论得到单调区间。
(2)在第一问的基础上,利用函数的单调性确定极值问题。
解:由已知得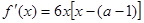 ,令
,令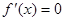 ,解得
,解得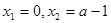 。。。。。。。2分
。。。。。。。2分
(Ⅰ)当 时,
时,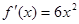 ,
, 在
在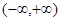 上单调递增;。。。。。。。。。。。4分
上单调递增;。。。。。。。。。。。4分
当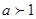 时,
时, 在
在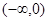 上单调递增;在
上单调递增;在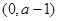 上单调递减;在
上单调递减;在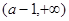 上单调递增;.。。。6
上单调递增;.。。。6
(Ⅱ)由(Ⅰ)知,当 时,函数
时,函数 没有极值;.。。。。。。。。。。。。。。。。。9分
没有极值;.。。。。。。。。。。。。。。。。。9分
当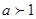 时,函数
时,函数 在
在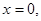 处取得极大值,在
处取得极大值,在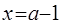 处取得极小值
处取得极小值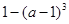 .。。。。。。。。12分
.。。。。。。。。12分
考点:本题主要考查了导数在研究函数中的运用。
点评:解决该试题的关键是利用导数来判定函数的单调性以及函数的极值问题,也是高考中常见的重要的题型,要给予关注。

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
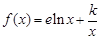 (其中e是自然对数的底数,k为正数)
(其中e是自然对数的底数,k为正数) 在
在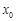 处取得极值,且
处取得极值,且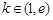 ,求
,求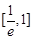 上的最大值.
上的最大值.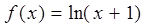
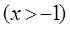

 的单调性。
的单调性。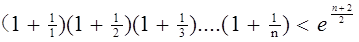
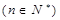
 ,
,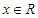 ,
,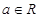 .
.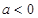 时,若函数
时,若函数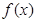 在区间
在区间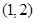 上是单调增函数,试求
上是单调增函数,试求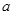 的取值范围;
的取值范围;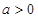 时,直接写出(不需给出演算步骤)函数
时,直接写出(不需给出演算步骤)函数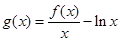 (
(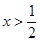 )的单调增区间;
)的单调增区间;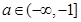 ,使函数
,使函数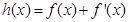 ,
,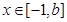 (
(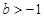 )在
)在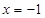 处取得最小值,试求实数
处取得最小值,试求实数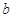 的最大值.
的最大值.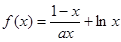
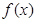 在
在 上为增函数,求正实数
上为增函数,求正实数 的取值范围;
的取值范围;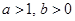 ,求证:
,求证: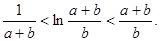
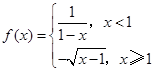 ,
,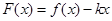 ,x∈R.试讨论函数F(x)的单调性.
,x∈R.试讨论函数F(x)的单调性. 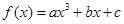
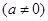 为奇函数,其图象在点
为奇函数,其图象在点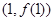 处的切线与直线
处的切线与直线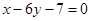 垂直,导函数
垂直,导函数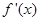 的最小值为
的最小值为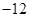 .试求
.试求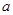 ,
, ,
,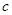 的值。
的值。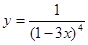 的导数.
的导数.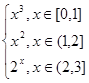 在区间[0,3]上的积分.
在区间[0,3]上的积分.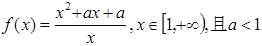
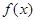 的单调性并证明;
的单调性并证明;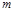 满足
满足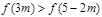 ,试确定
,试确定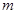 的取值范围。
的取值范围。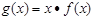 对任意
对任意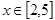 时,
时,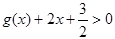 恒成立,求
恒成立,求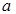 的取值范围。
的取值范围。