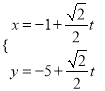题目内容
【题目】已知方程(x2﹣2x+m)(x2﹣2x+n)=0的四个根组成一个首项为 ![]() 的等差数列,则|m﹣n|等于( )
的等差数列,则|m﹣n|等于( )
A.1
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:设4个根分别为x1、x2、x3、x4 , 则x1+x2=2,x3+x4=2,
由等差数列的性质,当m+n=p+q时,am+an=ap+aq .
设x1为第一项,x2必为第4项,可得数列为 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴m= ![]() ,n=
,n= ![]() .
.
∴|m﹣n|= ![]() .
.
故选C
【考点精析】通过灵活运用解一元二次不等式和等差数列的性质,掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列即可以解答此题.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列即可以解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目