题目内容
设动点P(x,y)(y≥0)到定点F(0,1)的距离比它到x轴的距离大1,记点P的轨迹为曲线C.(Ⅰ)求点P的轨迹方程;
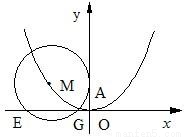
(Ⅱ)设圆M过A(0,2),且圆心M在曲线C上,EG是圆M在x轴上截得的弦,试探究当M运动时,弦长|EG|是否为定值?为什么?
【答案】分析:(Ⅰ)由题意知,P的轨迹满足抛物线的定义,故可求出抛物线的焦点,继而求出抛物线方程.
(Ⅱ)待定系数法设出圆的方程,设出圆与x轴的两个焦点E,G的坐标,再根据圆心在抛物线上,将圆心坐标代入抛物线,两个式子联立可求出x1-x2是否为定值.
解答:解:(Ⅰ)依题意知,动点P到定点F(0,1)的距离等于P到直线y=-1的距离,
曲线C是以原点为顶点,F(0,1)为焦点的抛物线
∵
∴p=2
∴曲线C方程是x2=4y
(Ⅱ)设圆的圆心为M(a,b),
∵圆M过A(0,2),
∴圆的方程为 (x-a)2+(y-b)2=a2+(b-2)2
令y=0得:x2-2ax+4b-4=0
设圆与x轴的两交点分别为(x1,0),(x2,0)
不妨设x1>x2,由求根公式得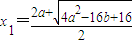 ,
,
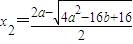
∴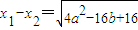
又∵点M(a,b)在抛物线x2=4y上,
∴a2=4b,
∴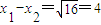 ,
,
即|EG|=4
∴当M运动时,弦长|EG|为定值4
点评:本题考查圆与抛物线相交关系的应用,考查了圆的定义,抛物线的定义,以及点的轨迹方程的求法,属于难题.
(Ⅱ)待定系数法设出圆的方程,设出圆与x轴的两个焦点E,G的坐标,再根据圆心在抛物线上,将圆心坐标代入抛物线,两个式子联立可求出x1-x2是否为定值.
解答:解:(Ⅰ)依题意知,动点P到定点F(0,1)的距离等于P到直线y=-1的距离,
曲线C是以原点为顶点,F(0,1)为焦点的抛物线
∵

∴p=2
∴曲线C方程是x2=4y
(Ⅱ)设圆的圆心为M(a,b),
∵圆M过A(0,2),
∴圆的方程为 (x-a)2+(y-b)2=a2+(b-2)2
令y=0得:x2-2ax+4b-4=0
设圆与x轴的两交点分别为(x1,0),(x2,0)
不妨设x1>x2,由求根公式得
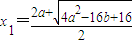 ,
,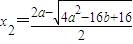
∴
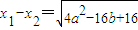
又∵点M(a,b)在抛物线x2=4y上,
∴a2=4b,
∴
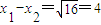 ,
,即|EG|=4
∴当M运动时,弦长|EG|为定值4
点评:本题考查圆与抛物线相交关系的应用,考查了圆的定义,抛物线的定义,以及点的轨迹方程的求法,属于难题.

练习册系列答案
相关题目
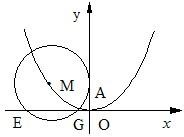 设动点P(x,y)(y≥0)到定点F(0,1)的距离比它到x轴的距离大1,记点P的轨迹为曲线C.
设动点P(x,y)(y≥0)到定点F(0,1)的距离比它到x轴的距离大1,记点P的轨迹为曲线C.