题目内容
设动点P(x,y)(y≥0)到定点F(0,1)的距离比它到x轴的距离大1,记点P的轨迹为曲线C.
(1)求点P的轨迹方程;
(2)若圆心在曲线C上的动圆M过点A(0,2),试证明圆M与x轴必相交,且截x轴所得的弦长为定值.
(1)求点P的轨迹方程;
(2)若圆心在曲线C上的动圆M过点A(0,2),试证明圆M与x轴必相交,且截x轴所得的弦长为定值.
分析:(1)由题意知,P的轨迹满足抛物线的定义,故可求出抛物线的焦点,继而求出抛物线方程.
(2)待定系数法设出圆的方程,设出圆与x轴的两个焦点E,G的坐标,再根据圆心在抛物线上,将圆心坐标代入抛物线,利用弦长公式及韦达定理可求结论.
(2)待定系数法设出圆的方程,设出圆与x轴的两个焦点E,G的坐标,再根据圆心在抛物线上,将圆心坐标代入抛物线,利用弦长公式及韦达定理可求结论.
解答: 解:(1)依题意知,动点P到定点F(0,1)的距离等于P到直线y=-1的距离,
解:(1)依题意知,动点P到定点F(0,1)的距离等于P到直线y=-1的距离,
曲线C是以原点为顶点,F(0,1)为焦点的抛物线
∵
=1,∴p=2,
∴曲线C方程是x2=4y …(5分)
(2)设圆心为M(a,b),
∵圆M过A(0,2),
∴圆的方程为 (x-a)2+(y-b)2=a2+(b-2)2
令y=0得:x2-2ax+4b-4=0
∵点M(a,b)在抛物线x2=4y上,
∴a2=4b,
∴△=4a2-16b+16>0
∴圆M与x轴必相交 …(9分)
设圆M与x轴的两交点分别为E(x1,0),G(x2,0)
∵x1+x2=2a,x1x2=4b-4
∴|EG|2=(x1+x2)2-4x1x2=4a2-16b+16=16
∴|EG|=4
∴当M运动时,弦长|EG|为定值4 …(13分)
 解:(1)依题意知,动点P到定点F(0,1)的距离等于P到直线y=-1的距离,
解:(1)依题意知,动点P到定点F(0,1)的距离等于P到直线y=-1的距离,曲线C是以原点为顶点,F(0,1)为焦点的抛物线
∵
| p |
| 2 |
∴曲线C方程是x2=4y …(5分)
(2)设圆心为M(a,b),
∵圆M过A(0,2),
∴圆的方程为 (x-a)2+(y-b)2=a2+(b-2)2
令y=0得:x2-2ax+4b-4=0
∵点M(a,b)在抛物线x2=4y上,
∴a2=4b,
∴△=4a2-16b+16>0
∴圆M与x轴必相交 …(9分)
设圆M与x轴的两交点分别为E(x1,0),G(x2,0)
∵x1+x2=2a,x1x2=4b-4
∴|EG|2=(x1+x2)2-4x1x2=4a2-16b+16=16
∴|EG|=4
∴当M运动时,弦长|EG|为定值4 …(13分)
点评:本题考查圆与抛物线相交关系的应用,考查了圆的定义,抛物线的定义,以及点的轨迹方程的求法,考查运算求解能力,中等题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
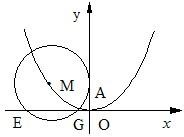 设动点P(x,y)(y≥0)到定点F(0,1)的距离比它到x轴的距离大1,记点P的轨迹为曲线C.
设动点P(x,y)(y≥0)到定点F(0,1)的距离比它到x轴的距离大1,记点P的轨迹为曲线C.