题目内容
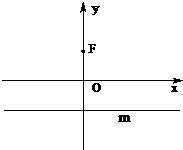（2013•嘉定区二模）如图，已知点F（0，1），直线m：y=-1，P为平面上的动点，过点P作m的垂线，垂足为点Q，且| QP |
| QF |
| FP |
| FQ |
（1）求动点P的轨迹C的方程；
（2）（理）过轨迹C的准线与y轴的交点M作直线m′与轨迹C交于不同两点A、B，且线段AB的垂直平分线与y轴的交点为D（0，y0），求y0的取值范围；
（3）（理）对于（2）中的点A、B，在y轴上是否存在一点D，使得△ABD为等边三角形？若存在，求出点D的坐标；若不存在，请说明理由．
分析：（1）设P（x，y），由题意得Q（x，-1），即可得到
，
，
，
，利用向量的数量积运算即可得出动点P的轨迹C的方程；
（2）利用（1）的轨迹方程即可得到准线方程及点M的坐标，设直线m'的方程为y=kx-1（k≠0），与抛物线方程联立得到根与系数的关系，利用中点坐标和垂直平分线的性质即可得到线段AB的垂直平分线的方程即可；
（3）利用（2）的结论，点到直线的距离公式及等边三角形的判定即可得出．
| QP |
| QF |
| FP |
| FQ |
（2）利用（1）的轨迹方程即可得到准线方程及点M的坐标，设直线m'的方程为y=kx-1（k≠0），与抛物线方程联立得到根与系数的关系，利用中点坐标和垂直平分线的性质即可得到线段AB的垂直平分线的方程即可；
（3）利用（2）的结论，点到直线的距离公式及等边三角形的判定即可得出．
解答：解：（1）设P（x，y），由题意，Q（x，-1），
=(0 ， y+1)，
=(-x ， 2)，
=(x ， y-1)，
=(x ， -2)，
由
•
=
•
，得2（y+1）=x2-2（y-1），
化简得x2=4y．所以，动点P的轨迹C的方程为x2=4y．
（2）轨迹C为抛物线，准线方程为y=-1，
即直线m，∴M（0，-1），
设直线m'的方程为y=kx-1（k≠0），由
得x2-4kx+4=0，
由△=16k2-16＞0，得k2＞1．
设A（x1，y1），B（x2，y2），则x1+x2=4k，
所以线段AB的中点为（2k，2k2-1），
所以线段AB垂直平分线的方程为（x-2k）+k[y-（2k2-1）]=0，
令x=0，得y0=2k2+1．
因为k2＞1，所以y0∈（3，+∞）．
（3）由（2），x1+x2=4k，x1x2=4，
∴|AB|=
=
=
=
=4
．
假设存在点D（0，y0），使得△ABD为等边三角形，
则D到直线AB的距离d=
|AB|．
因为D（0，2k2+1），所以d=
=
=2
，
所以2
=2
•
，解得k2=
．
所以，存在点D(0 ，
)，使得△ABD为等边三角形．
| QP |
| QF |
| FP |
| FQ |
由
| QP |
| QF |
| FP |
| FQ |
化简得x2=4y．所以，动点P的轨迹C的方程为x2=4y．
（2）轨迹C为抛物线，准线方程为y=-1，
即直线m，∴M（0，-1），
设直线m'的方程为y=kx-1（k≠0），由
|
由△=16k2-16＞0，得k2＞1．
设A（x1，y1），B（x2，y2），则x1+x2=4k，
所以线段AB的中点为（2k，2k2-1），
所以线段AB垂直平分线的方程为（x-2k）+k[y-（2k2-1）]=0，
令x=0，得y0=2k2+1．
因为k2＞1，所以y0∈（3，+∞）．
（3）由（2），x1+x2=4k，x1x2=4，
∴|AB|=
| (x1-x2)2+(y1-y2)2 |
| (1+k2)(x1-x2)2 |
| (1+k2)[(x1+x2)2-4x1x2] |
=
| (1+k2)(16k2-16) |
| (k2+1)(k2-1) |
假设存在点D（0，y0），使得△ABD为等边三角形，
则D到直线AB的距离d=
| ||
| 2 |
因为D（0，2k2+1），所以d=
| |y0+1| | ||
|
| 2(k2+1) | ||
|
| k2+1 |
所以2
| k2+1 |
| 3 |
| k2+1 |
| k2-1 |
| 4 |
| 3 |
所以，存在点D(0 ，
| 11 |
| 3 |
点评：本题主要考查抛物线的方程与性质、向量的数量积、准线与抛物线相交问题转化为方程联立得到根与系数的关系、弦长公式、等边三角形的定义、点到直线的距离公式、线段的垂直平分线及对称等基础知识，考查运算能力、推理论证以及分析问题、解决问题的能力．
练习册系列答案
相关题目