题目内容
(2013•楚雄州模拟)在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x、y,设O为坐标原点,点P的坐标为(x-2,x-y).
(1)求|OP|的最大值;
(2)求|OP|取得最大值时的概率.
(1)求|OP|的最大值;
(2)求|OP|取得最大值时的概率.
分析:(1)利用两点间的距离公式及x、y的取值即可得到最大值;
(2)利用(1)先求出|OP|取得最大值时的包括的基本事件的个数,再求出基本事件的总数,利用古典概型的概率计算公式即可得出.
(2)利用(1)先求出|OP|取得最大值时的包括的基本事件的个数,再求出基本事件的总数,利用古典概型的概率计算公式即可得出.
解答:解:(1)∵x、y可能的取值为1、2、3,∴|x-2|≤1,|y-x|≤2,
∴|OP|=
≤
=
,且当x=1,y=3或x=3,y=1时,|OP|=
. 因此,|OP|最大值为
.
(2)有放回抽两张卡片的所有情况有3×3=9种,而由(1)可知:取得最大值时只有两种情况:x=1,y=3,或x=3,y=1.
∴|OP|取得最大值时的概率P=
.
∴|OP|=
| (x-2)2+(x-y)2 |
| 12+22 |
| 5 |
| 5 |
| 5 |
(2)有放回抽两张卡片的所有情况有3×3=9种,而由(1)可知:取得最大值时只有两种情况:x=1,y=3,或x=3,y=1.
∴|OP|取得最大值时的概率P=
| 2 |
| 9 |
点评:熟练掌握两点间的距离公式、古典概型的概率计算公式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
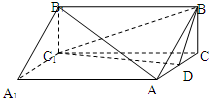 (2013•楚雄州模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=2,AA1=3,D为AC的中点.
(2013•楚雄州模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=2,AA1=3,D为AC的中点.