题目内容
(2013•楚雄州模拟)已知a,b∈(0,+∞)且2a+b=1,则s=2
-4a2-b2的最大值为( )
| ab |
分析:利用基本不等式的性质即可得出.
解答:解:∵a,b∈(0,+∞)且2a+b=1,
∴s=2
-4a2-b2=
-[(2a)2+b2]≤
×
-
=
.
当且仅当2a=b=
时取等号,故s的最大值是
.
故选A.
∴s=2
| ab |
| 2 |
| 2ab |
| 2 |
| 2a+b |
| 2 |
| (2a+b)2 |
| 2 |
| ||
| 2 |
当且仅当2a=b=
| 1 |
| 2 |
| ||
| 2 |
故选A.
点评:熟练掌握基本不等式的性质及其变形是解题的关键.

练习册系列答案
相关题目
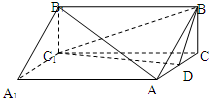 (2013•楚雄州模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=2,AA1=3,D为AC的中点.
(2013•楚雄州模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=2,AA1=3,D为AC的中点.