题目内容
已知α、β均为锐角，且sin2α=sin（α-β），则α、β的大小关系是（ ）
| A、α＞β | B、α＜β | C、α≤β | D、α与β的大小不确定 |
分析：先利用余弦函数的两角和公式对题设等式化简整理后sinα-sinβ=
，进而根据α，β的范围确定cosα，cosβ，sinα都大于0
进而推断出sinα-sinβ＞0，利用正弦函数的单调性求得a和β的大小关系．
| cosαcosβ |
| sinα |
进而推断出sinα-sinβ＞0，利用正弦函数的单调性求得a和β的大小关系．
解答：解：cos（α-β）=cosα•cosβ+sinα•sinβ=sin2α
∴cosα•cosβ=sin2α-sinα•sinβ=sinα（sinα-sinβ）
即sinα-sinβ=
∵α，β为锐角，∴cosα，cosβ，sinα都大于0
即sinα-sinβ＞0
y=sinx 第一象限为增函数
∴α＞β
故选A
∴cosα•cosβ=sin2α-sinα•sinβ=sinα（sinα-sinβ）
即sinα-sinβ=
| cosαcosβ |
| sinα |
∵α，β为锐角，∴cosα，cosβ，sinα都大于0
即sinα-sinβ＞0
y=sinx 第一象限为增函数
∴α＞β
故选A
点评：本题主要考查了三角函数的最值问题，两角和与差的余弦函数．考查了学生综合性的分析问题和转化和化归的数学思想的运用．
练习册系列答案
相关题目
，
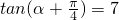，α，β均为锐角．
，
，α，β均为锐角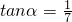
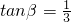,cos(α+β)=
,α,β均为锐角，求β的值.
如图，点B在以PA为直径的圆周上，点C在线段AB上，已知
，设
，
均为锐角.
；
的数量积
的值.
如图，点B在以PA为直径的圆周上，点C在线段AB上，已知
，设
，
均为锐角.
；
的数量积
的值.