题目内容
命题“若△ABC不是等腰三角形,则它的任何两个内角不相等.”的逆否命题是( )
| A.“若△ABC是等腰三角形,则它的任何两个内角相等” |
| B.“若△ABC任何两个内角不相等,则它不是等腰三角形” |
| C.“若△ABC有两个内角相等,则它是等腰三角形” |
| D.“若△ABC任何两个角相等,则它是等腰三角形” |
C
解析试题分析:根据命题的逆否命题的定义是对条件、结论同时否定,并把条件和结论胡换位置,
∴命题“若△ABC不是等腰三角形,则它的任何两个内角不相等”的逆否命题是“若△ABC的两个内角相等,则它是等腰三角形”,
故答案为:若△ABC的两个内角相等,则它是等腰三角形.
考点:四种命题
点评:本题考查命题的逆否命题的形式:对条件、结论同时否定并交换位置.注意分清命题的条件和结论.属基础题.

练习册系列答案
相关题目
已知P: 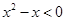 ,那么P的一个必要不充分条件是( )
,那么P的一个必要不充分条件是( )
A.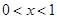 | B.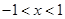 | C.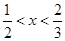 | D. |
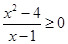 成立的一个必要不充分条件是( )
成立的一个必要不充分条件是( )
A.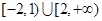 | B.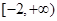 |
C.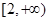 | D.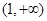 |
下列命题中正确的是( )
A.命题“若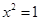 ,则 ,则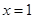 ”的否命题为“若 ”的否命题为“若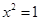 ,则 ,则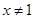 ” ” |
B.“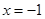 ”是“ ”是“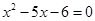 ”的必要不充分条件 ”的必要不充分条件 |
C.命题“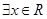 ,使得 ,使得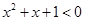 ”的否定是“ ”的否定是“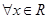 ,均有 ,均有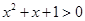 ” ” |
D.命题“在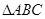 中,若 中,若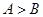 ,则 ,则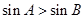 ”的逆否命题为真命题 ”的逆否命题为真命题 |
已知圆 的极坐标方程为
的极坐标方程为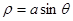 ,则“
,则“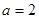 ”是“圆
”是“圆 与极轴所在直线相切”的 ( )
与极轴所在直线相切”的 ( )
| A.充分不必要条件. | B.必要不充分条件. |
| C.充要条件. | D.既不充分又不必要条件. |
“若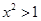 ,则
,则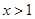 或
或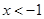 ”的否命题为( )
”的否命题为( )
A.若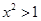 ,则 ,则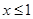 或 或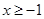 |
B.若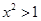 ,则 ,则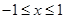 |
C.若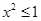 , 则 , 则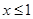 或 或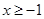 |
D.若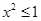 ,则 ,则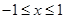 |
命题“若x2+y2=0,则x、y全为0”的逆否命题是
| A.若x、y全为0,则x2+y2≠0 | B.若x、y不全为0,则x2+y2=0 |
| C.若x、y全不为0,则x2+y2≠0 | D.若x、y不全为0,则x2+y2≠0 |
下列命题中:
①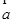 ∥
∥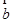
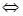 存在唯一的实数
存在唯一的实数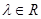 ,使得
,使得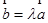 ;
;
②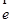 为单位向量,且
为单位向量,且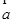 ∥
∥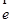 ,则
,则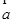 =±|
=±|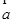 |·
|·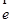 ;③
;③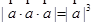 ;
;
④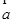 与
与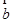 共线,
共线,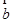 与
与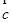 共线,则
共线,则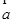 与
与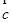 共线;⑤若
共线;⑤若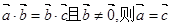
其中正确命题的序号是 ( )
| A.①⑤ | B.②③④ |
| C.②③ | D.①④⑤ |
已知命题p:函数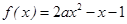 (a≠0)在(0,1)内恰有一个零点;命题q:函数
(a≠0)在(0,1)内恰有一个零点;命题q:函数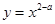 在(0,+
在(0,+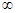 )上是减函数.若p且
)上是减函数.若p且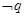 为真命题,则实数a的取值范围是( )
为真命题,则实数a的取值范围是( )
| A.a>1 | B.a≤2 | C.1<a≤2 | D.a≤l或a>2 |