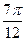题目内容
已知:向量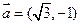 ,
,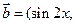
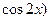 ,函数
,函数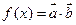 ,若
,若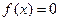 且
且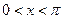
 ,求
,求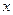 的值;
的值;
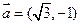 ,
,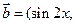
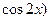 ,函数
,函数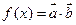 ,若
,若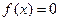 且
且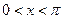
 ,求
,求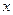 的值;
的值; 或
或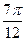
先由向量运算得出三角函数间的关系,再进一步处理。∵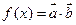 =
= -
-
由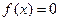 得
得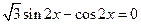 即
即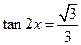
∵
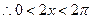 ∴
∴ 或
或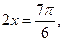
∴ 或
或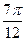
给式求角问题可考虑先求出一种三角函数值,再精确估计角的范围再定角。
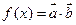 =
= -
-由
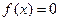 得
得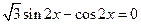 即
即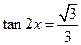
∵

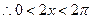 ∴
∴ 或
或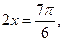
∴
 或
或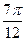
给式求角问题可考虑先求出一种三角函数值,再精确估计角的范围再定角。

练习册系列答案
相关题目
题目内容
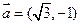 ,
,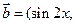
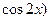 ,函数
,函数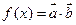 ,若
,若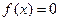 且
且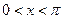
 ,求
,求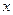 的值;
的值; 或
或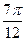
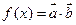 =
= -
-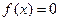 得
得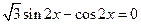 即
即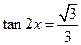

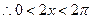 ∴
∴ 或
或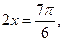
 或
或