题目内容
如图1,直角梯形ABCD中,AD∥BC,AD⊥CD,AD=2BC=2CD=4,E为AD的中点,将△ABE沿BE折起,使二面角A-BE-C是直二面角,并连接AC,AD得到四棱锥A-BCDE,如图2.
(1)求四棱锥A-BCDE的体积;
(2)若M,N分别是BC,AD的中点,求证:MN∥平面ABE.

(1)求四棱锥A-BCDE的体积;
(2)若M,N分别是BC,AD的中点,求证:MN∥平面ABE.

分析:根据折起后几何图形的性质,判断椎体的高与底面,根据椎体的体积公式求解即可;
根据平行四边形的对边平行且相等,判定线线平行,再通过线线平行证线面平行.
根据平行四边形的对边平行且相等,判定线线平行,再通过线线平行证线面平行.
解答: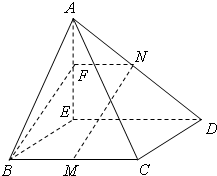 解:(1)∵AD=2BC=4,E为AD的中点,∴BE∥CD
解:(1)∵AD=2BC=4,E为AD的中点,∴BE∥CD
又∵AD⊥CD∴BE⊥AE,BE⊥ED∴∠AED是二面角A-BE-C所成的二面角,即∠AED=90°
而BE∩ED=E,BE,ED⊆平面BCDE∴AE⊥平面BCDE∵AE=2,SBCDE=4∴四棱锥A-BCDE的体积V=
.
(2)证明:作AE的中点F,连接NF,BF
∵N是AD的中点,∴NF∥BC,NF=
BC
又∵M分别是BC的中点,∴BM∥NF,BM=NF,
∴四边形BMNF是平行四边形,∴MN∥BF
∵MN?平面ABE,BF?平面ABE,
∴MN∥平面ABE.
 解:(1)∵AD=2BC=4,E为AD的中点,∴BE∥CD
解:(1)∵AD=2BC=4,E为AD的中点,∴BE∥CD又∵AD⊥CD∴BE⊥AE,BE⊥ED∴∠AED是二面角A-BE-C所成的二面角,即∠AED=90°
而BE∩ED=E,BE,ED⊆平面BCDE∴AE⊥平面BCDE∵AE=2,SBCDE=4∴四棱锥A-BCDE的体积V=
| 8 |
| 3 |
(2)证明:作AE的中点F,连接NF,BF
∵N是AD的中点,∴NF∥BC,NF=
| 1 |
| 2 |
又∵M分别是BC的中点,∴BM∥NF,BM=NF,
∴四边形BMNF是平行四边形,∴MN∥BF
∵MN?平面ABE,BF?平面ABE,
∴MN∥平面ABE.
点评:本题考查椎体的体积计算与线面平行关系的证明.证明线面平行的方法:法一,线线平行⇒线面平行;法二,面面平行⇒线面平行.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
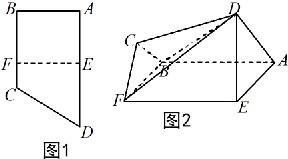 如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4.将四边形EFCD沿EF折起成如图2的位置,使AD=AE.
如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4.将四边形EFCD沿EF折起成如图2的位置,使AD=AE.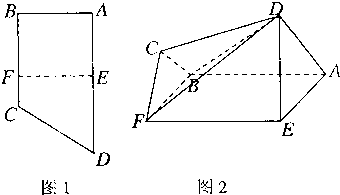 (2011•宁波模拟)如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4,将四边形EFCD沿EF折起如图2的位置,使AD=AE.
(2011•宁波模拟)如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4,将四边形EFCD沿EF折起如图2的位置,使AD=AE.
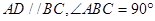 , E,F分别为边AD和BC上的点,且EF//AB,AD=2AE=2AB=4FC=4将四边形EFCD沿EF折起(如图2),使AD=AE.
, E,F分别为边AD和BC上的点,且EF//AB,AD=2AE=2AB=4FC=4将四边形EFCD沿EF折起(如图2),使AD=AE.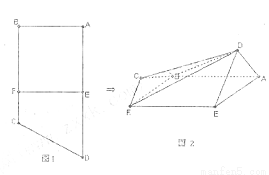
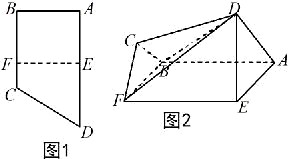 如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4.将四边形EFCD沿EF折起成如图2的位置,使AD=AE.
如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4.将四边形EFCD沿EF折起成如图2的位置,使AD=AE.