题目内容
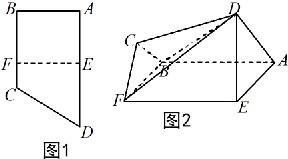 如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4.将四边形EFCD沿EF折起成如图2的位置,使AD=AE.
如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4.将四边形EFCD沿EF折起成如图2的位置,使AD=AE.(Ⅰ)求证:BC∥平面DAE;
(Ⅱ)求四棱锥D-AEFB的体积.
分析:(Ⅰ)先根据面面平行的判定定理,证得面CBF∥面DAE,又BC?面CBF,根据面面平行的性质可知BC∥平面DAE;
(Ⅱ)取AE的中点H,连接DH,根据线面垂直的判定定理可得EF⊥平面DAE,根据线面垂直的性质可知EF⊥DH,再根据AE=ED=DA=2∴DH⊥AE,DH=
,则DH⊥面AEFB,根据体积公式即可求出四棱锥D-AEFB的体积.
(Ⅱ)取AE的中点H,连接DH,根据线面垂直的判定定理可得EF⊥平面DAE,根据线面垂直的性质可知EF⊥DH,再根据AE=ED=DA=2∴DH⊥AE,DH=
| 3 |
解答:解:(Ⅰ)∵CF∥DE,FB∥AE,BF∩CF=F,AE∩DE=E
∴面CBF∥面DAE,又BC?面CBF,
所以BC∥平面DAE
(Ⅱ)取AE的中点H,连接DH,
∵EF⊥ED,EF⊥EA∴EF⊥平面DAE
又DH?平面DAE∴EF⊥DH,
∵AE=ED=DA=2∴DH⊥AE,DH=
∴DH⊥面AEFB,
所以四棱锥D-AEFB的体积V=
×
×2×2=
∴面CBF∥面DAE,又BC?面CBF,
所以BC∥平面DAE
(Ⅱ)取AE的中点H,连接DH,
∵EF⊥ED,EF⊥EA∴EF⊥平面DAE
又DH?平面DAE∴EF⊥DH,
∵AE=ED=DA=2∴DH⊥AE,DH=
| 3 |
∴DH⊥面AEFB,
所以四棱锥D-AEFB的体积V=
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
点评:本题主要考查棱锥的体积公式和线面平行的判定定理的应用.考查对定理的掌握情况和对基础知识的综合运用.

练习册系列答案
相关题目
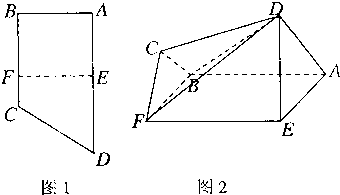 (2011•宁波模拟)如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4,将四边形EFCD沿EF折起如图2的位置,使AD=AE.
(2011•宁波模拟)如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4,将四边形EFCD沿EF折起如图2的位置,使AD=AE.
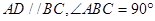 , E,F分别为边AD和BC上的点,且EF//AB,AD=2AE=2AB=4FC=4将四边形EFCD沿EF折起(如图2),使AD=AE.
, E,F分别为边AD和BC上的点,且EF//AB,AD=2AE=2AB=4FC=4将四边形EFCD沿EF折起(如图2),使AD=AE.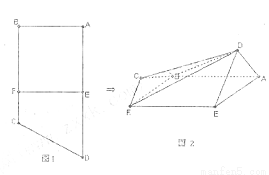
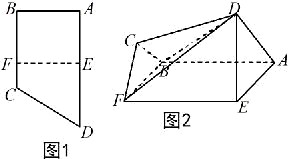 如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4.将四边形EFCD沿EF折起成如图2的位置,使AD=AE.
如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4.将四边形EFCD沿EF折起成如图2的位置,使AD=AE.